本文章为原创,版权归作者刘锦程所有,文章转载请先取得作者的同意,非常欢迎转发文章链接!严禁以任何方式挪用本文内容,用于以盈利为目的各种活动。
写在前面:在文章中用VASPKIT做自由能校正,建议引用参考
V. Wang, N. Xu, VASPKIT: A Pre- and Post-Processing Program for the VASP Code.
http://VASPKIT.sourceforge.net.
理论计算催化中的反应自由能变化是最为重要的内容,但是主流第一性原理计算程序(VASP, QE, CP2K等)都没有内置直接计算分子自由能的模块(注: 计算化学程序如Gaussian有很完善的自由能计算模块)。导致大量计算催化文献中的自由能校正方法不统一,不准确,甚至出现严重的定量错误(比如:比如ORR反应往往需要用实验值校正O2分子的自由能,某些文章计算出的总包反应能量和实验值偏差巨大,竟然审稿人看不出来问题,最后错误的结果发到JACS上)。
无论是气相化学反应,还是表面、材料的化学变化,都是在一定反应条件下进行的,但是直接用第一性原理程序计算出来的都是指在0K下忽略零点振动能(ZPE)的能量(俗称电子能量)。自由能校正中首先要计算配分函数,然后校正体系内能(U),焓(H),熵(S),ZPE。由此可以引入,反应温度、压力对能量的影响,从而可以进一步考虑 pH、电极电势等等外界因素对化学势的影响,讨论结果才和真实的实验情况更为接近。
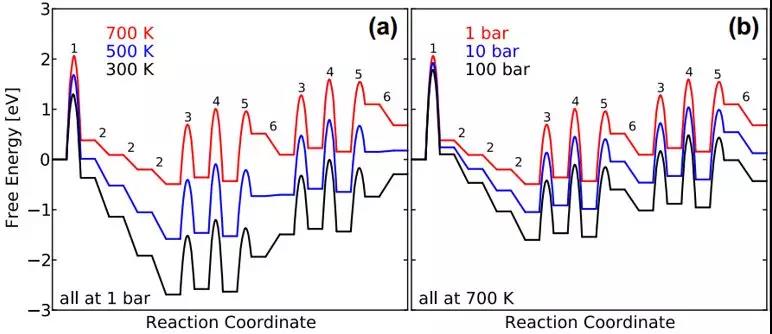
做自由能校正,对于催化反应过程的分析有重要意义。比如下图中的对合成氨反应在不同的温度和压强下做自由能变化图:(a)温度升高(300 K -> 700 K,1 bar),总反应的自由能从放热过程(自发)变为吸热过程(非自发)。(b)压强增大(1 bar -> 100 bar, 700 K),总反应的自由能从吸热过程变为放热过程。
配分函数(Partition function)
统计热力学中最关键的量是配分函数Q,
$$
Q=\sum_{i}^{\text { levels }} e^{-E_{i} / k T} \equiv \int_{0}^{\infty} \rho(E) e^{-E / k T} d E
$$
物理意义是体系的平均热可及的量子态数,由它可以得到各种热力学性质。计算中只能得到单个分子的性质,所以就需要把系综的配分函数和分子的配分函数联系起来。含N个分子的系综的配分函数Q与单个分子的配分函数q之间有如下关系:
$$
Q=\frac{q^{N}}{N !}
$$
$$
q=\sum_{i}^{\text { levels }} g_{i} e^{-\varepsilon_{i / k T}}
$$
借由分子配分函数将有大量组成成分(通常为分子)系统中微观物理状态(例如:动能、势能)与宏观物理量统计规律 (例如:压力、体积、温度、热力学函数、状态方程等)连结起来的科学。如气体分子系统中的压力、体积、温度。
一个分子的能量可以认为是由分子的整体运动的能量(平动能),以及分子内部运动的能量(转动能,振动能,电子激发能)之和:
\begin{equation}
\varepsilon_{\mathrm{tot}}=\varepsilon_{\mathrm{trans}}+\varepsilon_{\mathrm{rot}}+\varepsilon_{\mathrm{vib}}+\varepsilon_{\mathrm{ele}}
\end{equation}
所有热力学量都可以分解成这些组分的加和:
亥姆霍次自由能:
内能:
$$
U_{\mathrm{tot}}=U_{\mathrm{trans}}+U_{\mathrm{rot}}+U_{\mathrm{vib}}+U_{\mathrm{ele}}
$$
熵:
$$
S_{\mathrm{tot}}=S_{\mathrm{trans}}+S_{\mathrm{rot}}+S_{\mathrm{vib}}+S_{\mathrm{ele}}
$$
转动、振动、电子跃迁对U的贡献等价于对H的贡献,对Cv的贡献等价于对Cp的贡献。(只差一个PV或P),例如:
$$
\begin{array}{l}{H_{\text { trans }}=U_{\text { trans }}+\mathrm{PV}} \\ {C p_{\text { trans }}=C v_{\text { trans }}+\mathrm{P}}\end{array}
$$
气体分子的自由能校正
对气体分子做热力学量的校正需要包含有振动、平动、转动、电子激发对配分函数的贡献,得到配分函数以后带入到内能、焓、熵和配分函数的关系式中得到内能、焓、熵的校正值,再计算自由能的校正。这些过程涉及到较复杂的计算,好在VASPKIT已经把这所有的校正公式都编写好了,用的时候只需要气体分子的:
1,所有振动频率,
2,气体分压,
3,温度,
4,分子的基态多重度。
以VASP计算氧气分子自由能校正为例:
第一步:优化氧气分子的结构。
使用1 1 1的Gamma Center 的k点,
ISPIN = 2 (氧气分子是三重态),
ISYM = 0 (防止不合理的对称性导致错误的电子占据),
ISMEAR = 0;SIGMA = 0.01 (对于分子体系可以设置很小的sigma确保精度)
EDIFF = 1E-7 (保证精度高一些,因为频率计算和自由能校的精度对这两个参数极为敏感)
EDIFFG = -0.001
晶胞边长至少保证10 10 10 Angstrom。
第二步:计算氧气分子的振动频率。
修改以下INCAR参数:
IBRION = 5 或 6
NFREE = 2
POTIM = 0.015 (默认值)
EDIFF = 1E-7
计算完成以后grep cm OUTCAR,查看所有频率:
1 | [pg2059@ln4%cngrid2 o2]$ grep cm OUTCAR |
因为线性分子的振动自由度为(3N-5)。发现有三个虚频和两个非常小的频率,这是平动和转动在振动自由度上的投影,直接忽略即可(VASPKIT自动判断并忽略)。忽略最小的5个(线型分子)或6个(非线型分子)振动频率,并不是直接忽略了平动和转动的贡献。而是通过平动和转动的配分函数另外计算其对热力学量的贡献。其中平动熵是气体分子熵的主要贡献。
第三步:运行VASPKIT,使用主功能502。
VASPKIT
1 | 502 |
各种热力学量的校正值会直接打印在屏幕上:
Zero-point energy E_ZPE:零点振动能校正
Thermal correction to U(T):指定温度下的内能校正
$$
U(T)=U(0)+[U(T)-U(0)]=\varepsilon_{\mathrm{ele}}+\mathrm{ZPE}+\Delta U_{0 \rightarrow T}
$$Thermal correction to H(T):指定温度下的焓校正
$$
H(T)=H(0)+[H(T)-H(0)]=\varepsilon_{\mathrm{ele}}+\mathrm{ZPE}+\Delta H_{0 \rightarrow T}
$$Thermal correction to G(T):指定温度下的自由能校正
$$
G(T)=G(0)+[G(T)-G(0)]=\varepsilon_{\mathrm{ele}}+\mathrm{ZPE}+\Delta G_{0 \rightarrow T}
$$S(T) = - (G(T) - H(T))/T
注:一般文献中的表达,不把ZPE包含到内能校正中,所以G(T)可以写为如下内容:
$$
G(T)=E_{\mathrm{DFT}}+\mathrm{ZPE}+U(T)+TS(\mathrm{T})+PV
$$
其中:H(T) = U(T) + PV
注:文献中有的校正方法没有考虑U(T),用的公式是G(T) = EDFT + ZPE + TS + PV, 是因为这些文献的作者认为U(T)的贡献很小可以忽略,实际上,对于氧气分子这部分贡献有大约有H(298.15 K) = 0.161475 - 0.097144 = 0.064331 eV。查Janaf-NIST热力学表得到的 H(298.15 K) = 8.683 kJ/mol = 0.08999 eV, 由此可见对于精度要求稍高的计算,忽略H(T)都是不合理的做法。
用G(T)加上电子能量(结构优化OSZICAR中最后一个E0,或者频率计算中第一个E0的能量)值就是自由能校正之后的氧气分子的能量。
G(O2) = -9.863 + -0.447 = -10.310 eV
查JANAF-NIST表计算气体分子的自由能校正
我们也可以通过JANAF-NIST表来估算氧气分子的自由能校正值,比较我们用VASPKIT算出来的结果是否合理。
| Oxygen (O2) | O2(ref) | ||||||
|---|---|---|---|---|---|---|---|
| J·K-1 mol-1 | kJ·mol^-1^ | ||||||
| T/K | Cp° | S° | -[G°-H°(Tr)]/T | H-H°(Tr) | 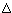 fH° fH° |
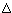 fG° fG° |
log Kf |
| 0 | 0. | 0. | INFINITE | -8.683 | 0. | 0. | 0. |
| 100 | 29.106 | 173.307 | 231.094 | -5.779 | 0. | 0. | 0. |
| 200 | 29.126 | 193.485 | 207.823 | -2.868 | 0. | 0. | 0. |
| 250 | 29.201 | 199.990 | 205.630 | -1.410 | 0. | 0. | 0. |
| 298.15 | 29.376 | 205.147 | 205.147 | 0. | 0. | 0. | 0. |
| 300 | 29.385 | 205.329 | 205.148 | 0.054 | 0. | 0. | 0. |
| 350 | 29.694 | 209.880 | 205.506 | 1.531 | 0. | 0. | 0. |
| 400 | 30.106 | 213.871 | 206.308 | 3.025 | 0. | 0. | 0. |
| 450 | 30.584 | 217.445 | 207.350 | 4.543 | 0. | 0. | 0. |
| 500 | 31.091 | 220.693 | 208.524 | 6.084 | 0. | 0. | 0. |
表中298.15 K下的
S(298.15 K) = 205.147 J·K-1·mol-1
H(298.15 K) - H(0 K) = 8.683 kJ·mol^-1^
G(298.15 K) = EDFT + ZPE + H(T) + TS(T) = -9.863 + 0.09714 + (8.683 x 0.01036427) - 298.15 x (205.147 x 0.0000103642723) = -10.3097 eV
由此可见,用vasp + VASPKIT得到的自由能和查找热力学表的实验值几乎完全一样,说明在高精度计算条件下,使用VASPKIT可以很好的校正气体分子的自由能。但是!这也有一部分误差抵消巧合的原因,vasp计算频率并不太准,尤其是低频振动,这会导致熵计算产生较大误差。另一部分误差的来源是电子能量的计算,也就是公式中的EDFT 。Norskov认为在ORR反应的计算中认为很难算准氧气分子的电子能量,所以需要用实验反应能量变化反推O2的能量,以满足总包反应的能量变化。
O2 + 2H2 -> H2O, G = -4.92 eV,
G(O2) = G(H2O) - 2G(H2) + 4.92
液体分子和溶质溶液的自由能计算
由于一些化学反应往往涉及到液相体系,比如电催化计算。所以算准溶液分子的能量也非常关键。
第一性原理计算对于校正溶剂化计算非常困难,目前已有的较准确的解决方案是用vaspsol或者用JDFTx的Candle模型,二者原理相似。
但是,实际上我们要想得到一个液体的自由能,并不需要直接计算溶剂化的分子。可以利用一些已知的实验数据,配合计算得到我们想要的自由能,这样比直接计算要准确的多:
技巧一:利用饱和蒸汽压下的气态和液态的化学势相等,可以通过计算气态分子在饱和蒸汽压下的自由能,即得到液体的自由能。这仅限于可以查得饱和蒸汽压的分子,比如我们常用得水分子,在常温下得饱和蒸汽压约为0.035 bar。在VASPKIT里计算分子自由能时候输入相应得压力就可以了。
技巧二:如果想要计算一个溶质的自由能那就没有这么简单了,比如我想知道 1mol/L 甲醇水溶液中甲醇的自由能,这时候此分压下的甲醇的蒸汽压就没这么容易可以查表得到,此时可以利用摩尔分数和分压的近似线性关系(实际上并不是完全线性的),来推得 1mol/L 甲醇水溶液中甲醇的自由能。
技巧三:如果想要计算水溶液中某离子的自由能,比如1mol/L Pt2+的自由能,那么直接计算离子的溶剂化能太困难了,可以利用的是标况下的标准电极电势。
$$
\mathrm{Pt}^{2+}(\mathrm{aq})+2 \mathrm{e}^{-} \Rightarrow \mathrm{Pt}(\mathrm{s}), U_{0}=+1.188 \mathrm{V}
$$
估计Pt bulk的能量很容易通过计算得到,那么标况下1mol/L Pt2+的自由能就带入下式得到。
$$
G\left(Pt^{2+}(a q)\right)=G(Pt(s))-2 e U_{0}
$$
表面吸附分子的自由能校正
不同于气态分子的热力学校正,表面吸附分子和载体形成化学键,从而限制了吸附分子的平动和转动自由度,所以平动和转动对于熵和焓的贡献都会显著降低(Hindered translator / hindered rotor model),但是这并不意味着没有贡献。一般大家都接受的方法(文献里最常用的方法)就是把这一部分贡献归到振动里,也就是说表面吸附分子的3N个振动(虚频除外)都用于计算热力学量的校正,而忽略表面受阻平动和受阻转动的实际的贡献。
注:想要精确计算表面分子受阻的平动和转动贡献,可以用ASE模块算,感兴趣的同学可以自己研究一下,ase.thermochemistry.HinderedThermo
第一步:优化吸附氧原子的Au(111)slab模型。
第二步:计算频率。固定所有Slab原子。因为固体的热力学量计算需要先计算声子谱,而VASP本身只能计算Gamma点的频率,所以把slab上的原子包含到频率计算里校正自由能没有意义,结果也不对。
查看频率结果:
1 | 1 f = 10.904836 THz 68.517103 2PiTHz 363.746154 cm-1 45.098792 meV |
发现三个实频。
如果计算的是O迁移的过渡态:
1 | 1 f = 12.609563 THz 79.228223 2PiTHz 420.609746 cm-1 52.148981 meV |
发现两个实频和一个虚频。计算自由能的时候不包括虚频。
第三步:启用VASPKIT,使用功能501。
1 | 501 |
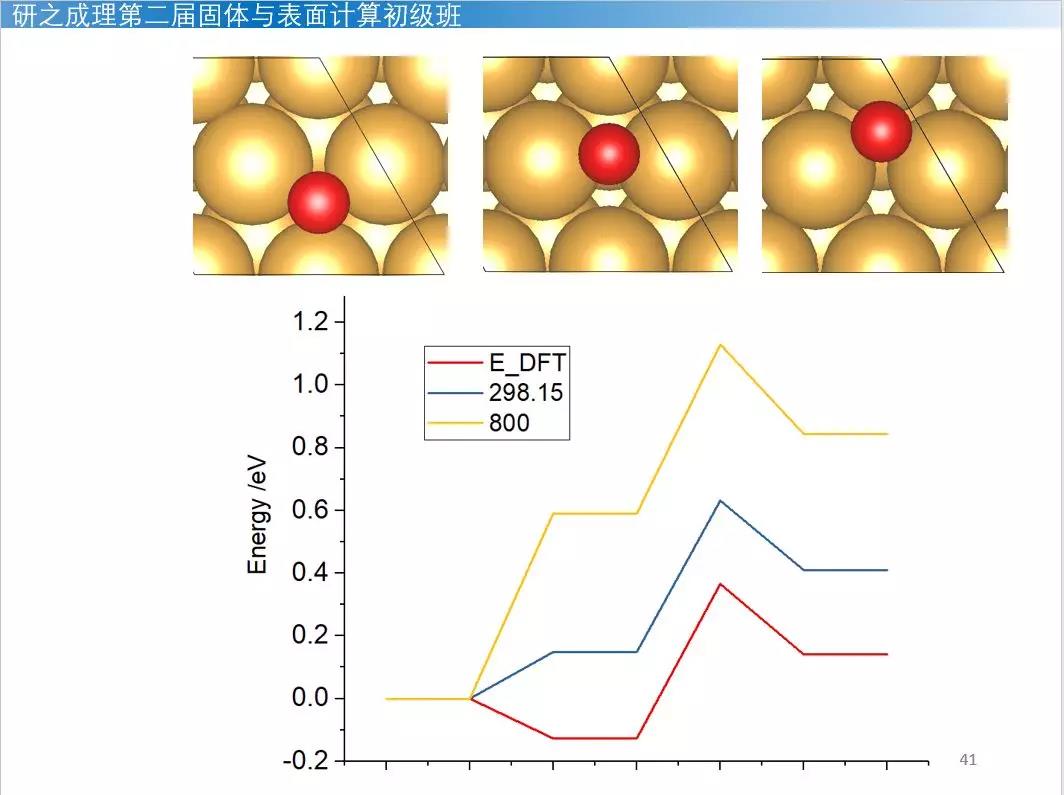
只需要输入温度即可,得到的G(T)就是吸附分子的自由能校正值0.052 eV,加上O/Au(111)优化的最后一个结构的能量就得到体系的自由能。同理可以对过渡态做自由能校正。对于如下反应可以画出如下反应的电子能量反应图和自由能反应图(不同温度298.15K,800K):
O2 + 2 -> 2O (adsorption)
O + -> + O (diffusion)
振动频率对于热力学量的贡献
可以以势能面最低点(Bottom of the well, BOT)为零点计算振动配分qvib , 此时谐振近似下的配分函数:
$$
q_{\mathrm{vib}}=\prod_{i} \frac{e^{-h v_{i} / 2 k T}}{1-e^{-h v_{i} / k T}}
$$
把配分函数qvib带入到各各热力学量里,内能校正:
$$
U_{\mathrm{vib}}(T)=R \sum_{i}\left(\frac{h v_{i}}{k}\right)\left(\frac{1}{2}+\frac{e^{-\frac{h v_{i}}{k T}}}{1-e^{-\frac{h v_{i}}{k T}}}\right).
$$
其中第一项是ZPE的贡献,第二项是从0K到T温度内能校正的贡献。0K时分子振动有零点振动能(ZPE),对应0K下(振动基态)时核振动的能量。注意:DFT计算出的能量不是体系在0K下的能量,而是体系在0K下并且忽略ZPE的能量。也就是说,实际分子在任何的状态下都存在ZPE。
ZPE和振动频率的关系:
频率越大的贡献越大,比如H2的伸缩振动频率有4395 cm−1,所以,H2参与的反应ZPE校正的能量就非常大。
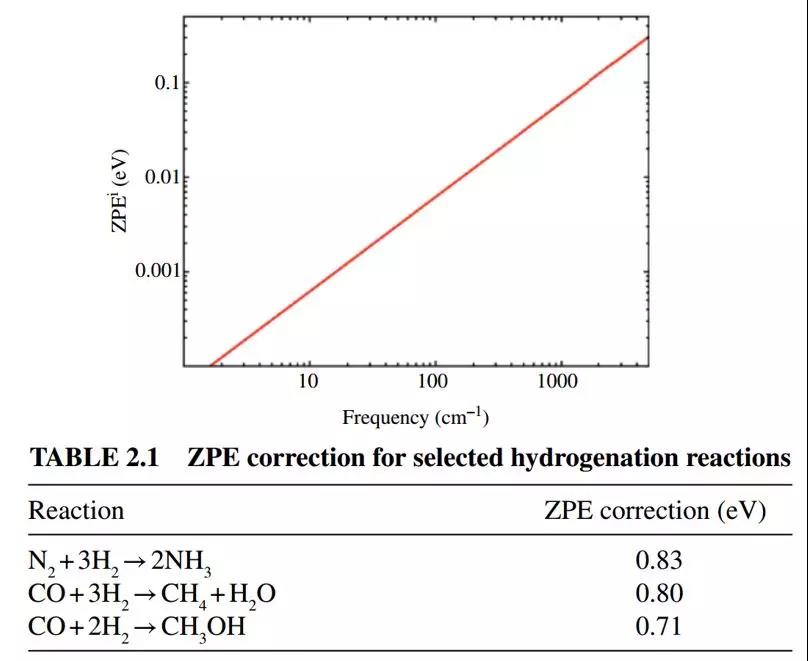
准确计算振动配分函数,特别是低频模式的贡献是准确计算热力学数据最关键也是最困难的地方。频率越低的振动模式对ZPE的贡献越小,但是由于对q_vib的贡献越大(因为更容易激发到其振动激发态),因此对升温造成的熵增贡献越大。
熵校正:
\begin{equation}
S_{\mathrm{vib}}(T)=R \sum_{i}\left\{\frac{h v_{i}}{k T} \frac{e^{-\frac{h v_{i}}{k T}}}{1-e^{-\frac{h v_{i}}{k T}}}-\ln \left[1-e^{-\frac{h v_{i}}{k T}}\right]\right\}
\end{equation}
可以看到,这里第一项正好和内能的第二项抵消,一些文章中的自由能校正不考虑H的贡献,是因为它抵消和熵的第一项。所以,只需要校正熵的第二项即可。
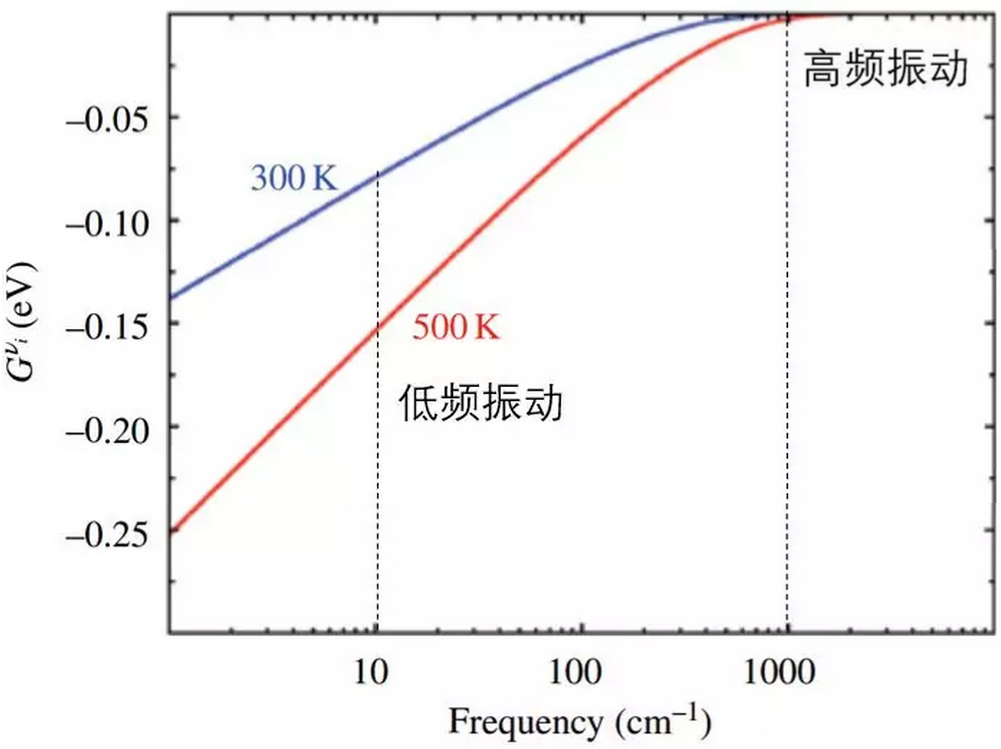
这是振动对熵的贡献关系图。温度越高,振动频率越小,校正的振动熵贡献越低。我们在做表面吸附分子的自由能计算时,分子的平动和转动的6个自由度被限制了,可以认为都变成了振动能量,这时候就很可能会出现小的振动频率使得校正出的自由能量异常的低,所以有的文献建议做表面吸附分子的自由能校正的时候,把频率在50 cm-1以下的贡献都算成是50 cm-1,VASPKIT也是这样做的,在文章的计算方法部分也要说明。
转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。