本文章为原创,版权归作者刘锦程所有,文章转载请先取得作者的同意,非常欢迎转发文章链接!严禁以任何方式挪用本文内容,用于以盈利为目的各种活动。
本帖使用目前最流行的COHP计算程序Lobster,可以配合VASP,QE,Abinit使用。这个帖子只简单的讲一些基本原理和案例,具体的Lobster使用方法以后有空再讲。
参考书:Roald Hoffman-Solids and Surfaces_ A Chemist’s View of Bonding in Extended Structures (1988)
参考文献:
J. Phys. Chem. 1993, 97, 8617-8624
J. Phys. Chem. A 2011, 115, 5461-5466
J. Comput. Chem. 2016, 37, 1030-1035
COOP
晶体轨道重叠布居 COOP(crystal orbital overlap population)的一个更为直观的名称是 重叠布居权重的态密度 (overlap population-weighted density of states)。
对于两个孤立的H原子的原子轨道可以用H原子的1s轨道基函数表示:
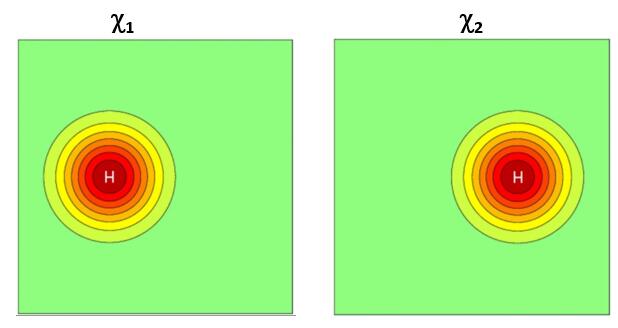
而两个氢原子靠近的时候,产生的分子轨道可以写成原子轨道线性组合的形式:
$$
\Phi=c_{1} \chi_{1}+c_{2} \chi_{2}
$$
对于任何的分子轨道波函数的线性展开:
$$
\Phi=c_{1} \chi_{1}+c_{2} \chi_{2} \dots
$$
假定展开基归一化但是不正交,此分子轨道中的电子分布由波函数的平方给出,因此:
$$
1=\int\left|\Phi^{2}\right| d \tau=\int\left|c_{1} \chi_{1}+c_{2} \chi_{2}\right|^{2} d \tau=c_{1}^{2}+c_{2}^{2}+2 c_{1} c_{2} S_{12}
$$
其中S12是重叠积分。上式表示分子轨道波函数中的一个电子是怎样分布的。
c12代表分配到中心1上的部分,c22表示分配到中心2上的部分,2c1c2S12是个和相互作用有关的量,称为重叠布局(overlap population)。(补充内容:按照mulliken的划分方法,把重叠布局等分到两个中心上的原子电荷是mulliken电荷, mulliken电荷是最简单的一种原子电荷。第一性原理计算中常用的原子电荷是Bader电荷,一种基于盆分析的原子电荷。)
如果c1c2同号,则重叠布居为正值(即成键),如果c1c2异号,则它为负值(即反键)。
重叠布居乘以相应的态密度,就可以得到重叠布居权重的态密度,简称COOP。
对COOP费米能级以下部分的积分值ICOOP可以理解为两个原子之间共享的成键电子的数目。在一定程度上可以反映出键强度的大小。
例一:一维氢原子链的DOS和COOP:
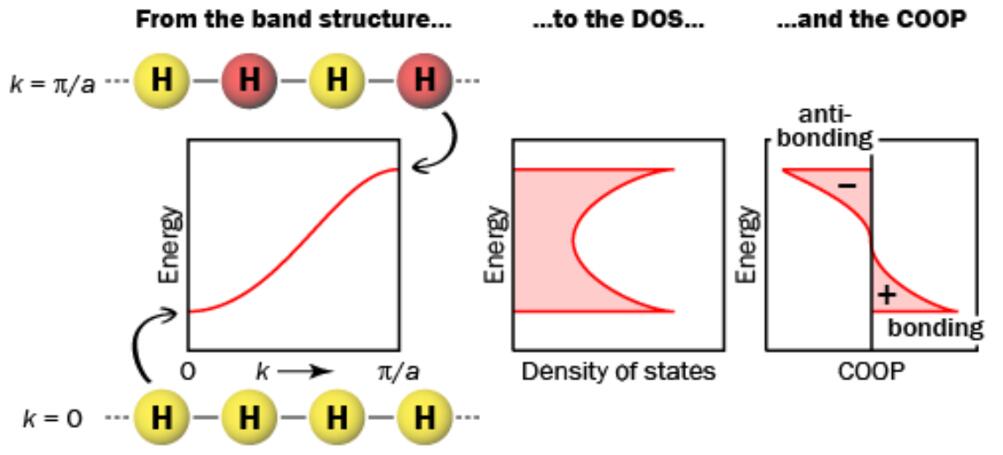
计算当中我们需要指定两个原子,计算这两个原子之间的COOP,例如对于一维的氢原子链,
当k = 0时(能带底端),相邻原子的波函数相位相同,COOP为正值;
当k = pi/a时(能带顶端),相邻原子的波函数相位相反,COOP为负值。
当k = pi/2a时(能带中间),重叠积分为0,COOP为0。
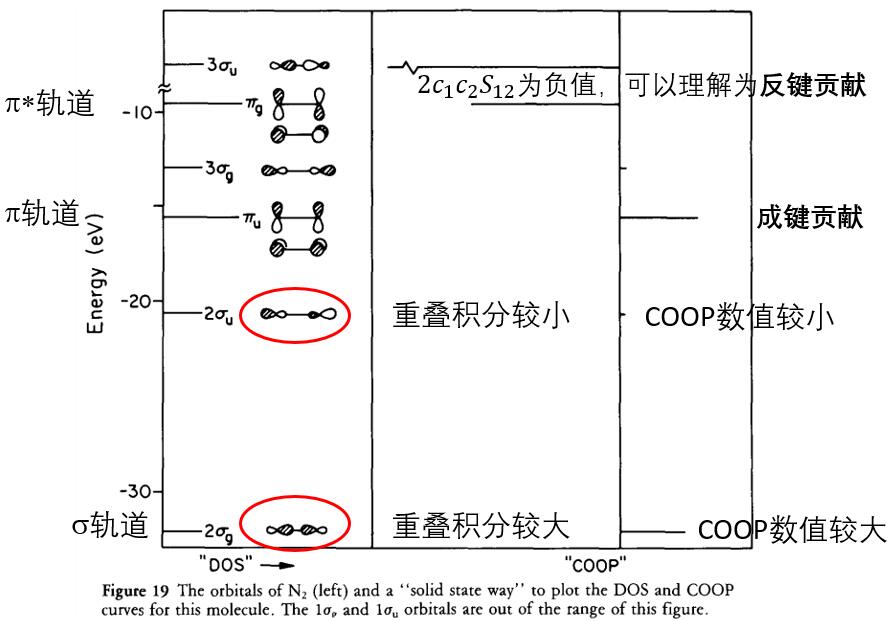
例二:N2分子的DOS和COOP:
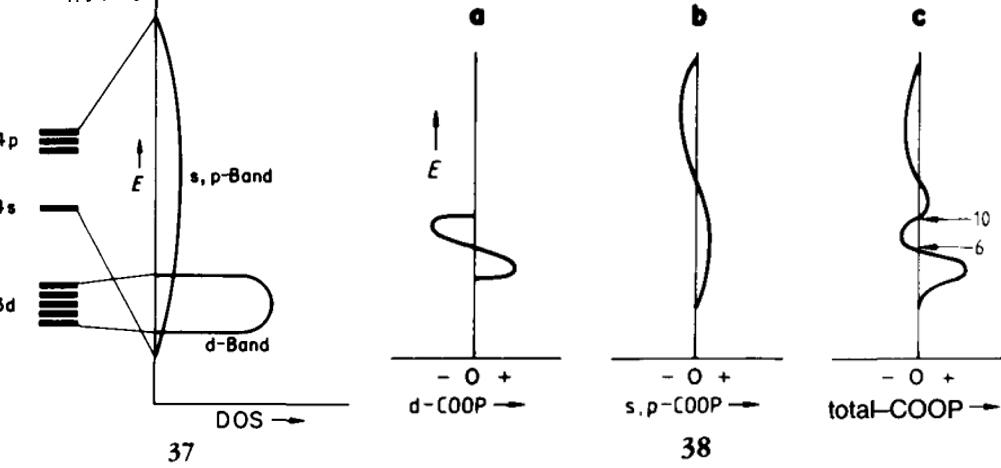
例三:过渡金属的COOP:
projected COOP (pCOOP) 和pDOS一样,同样可以对原子或者原子轨道做投影
过渡金属的d-band比较局域,而s和p-band比较弥散,所以,金属中相邻的金属元素做COOP计算,不同轨道的贡献范围有所不同,就导致总的COOP的成键和反键区域来回折返的情况:
COHP
COOP可以很好的研究周期性体系中的局域化学键性质,在上个世纪配合semiempirical extended Huckel (EH) theory取得了巨大的成功。
但是COOP还是存在一些问题:
COOP计算有很强的基组依赖性;在EH的理论框架下,如果研究p-p和d-d相互作用,由于原子轨道的空间延展方向,会有一定问题。
随着基于平面波基组的第一性原理计算的发展,COHP方法诞生,在1993年由Richard Dronskowski和Peter E.Blochl共同发表。
Richard Dronskowski就是我们之后要介绍的lobster程序的开发团队leader。
COHP的原理在Richard1993的文章中有详细的推导。简化来说就是把COOP中的重叠布居矩阵用哈密顿矩阵代替。
对于一个波函数,用LCAO写成原子轨道线性组合的形式:
$$
| \psi_{j} \rangle=\sum_{R L} | \chi_{R L} \rangle u_{R L, j}
$$
R代表原子,L代表原子轨道,j代表能带(分子轨道),
哈密顿矩阵元的形式:
$$
H_{R L, R L^{\prime}} \equiv\left\langle\chi_{R L}|\hat{H}| \chi_{R L^{\prime}}\right\rangle=\left\langle\chi_{R L}\left|-\nabla^{2}+v(\vec{r})\right| \chi_{R L^{\prime}}\right\rangle
$$
矩阵可以写成如下形式:
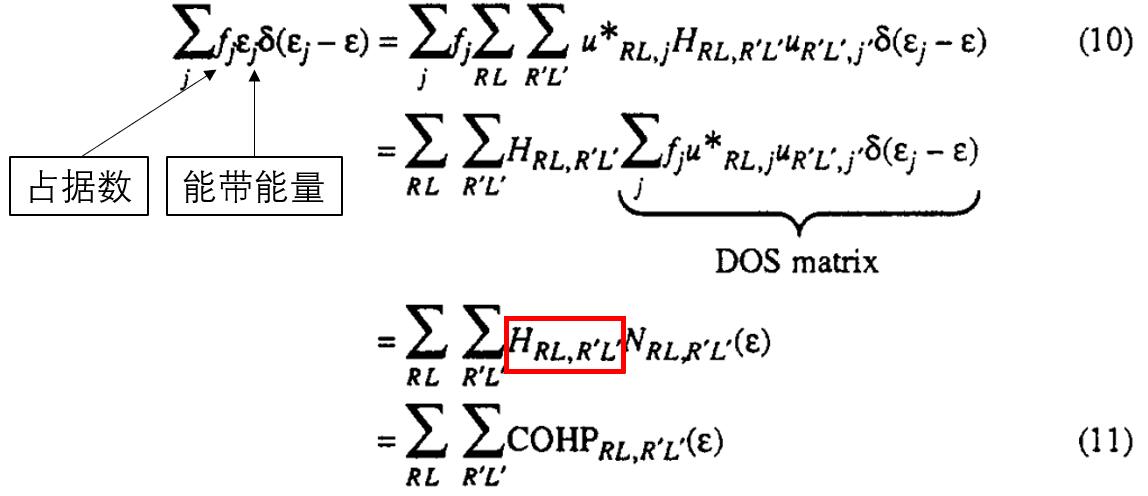
COHP和COOP的区别就是把原本的重叠矩阵替换成了哈密顿矩阵。同样要乘以一个DOS矩阵。所以,
COOP is weighted by the elements of the overlap matrix
COHP is weighted by the elements of the Hamiltonian matrix
再把该矩阵拆分成不同原子/轨道之间的贡献。原子对组成的矩阵的对角元属于原子的贡献(R = R’),这一部分我们不关心。
非对角元是原子之间的共价成分的贡献,分为成键贡献(即这一项使得总能降低),和反键贡献(即这一部分使得总能上升)。而且由于N(ε)是能量分辨的。所以和COOP一样,COHP可以画出类似的图像。
COHP处理平面波基组波函数
最初的COHP只能处理以原子为中心基函数的波函数,流行方法是linear muffin-tin orbital (LMTO) 或者Tight-Binding LMTO (TB-LMTO),这种方法基于中心化的局域基组,不适用与平面波基组。直到2011年Richard Dronskowski才发表一种将平面波基组投影到局域化的基组上的方法,并且开发了Lobster程序,用于处理VASP,QE,Abinit等平面波基组的波函数。
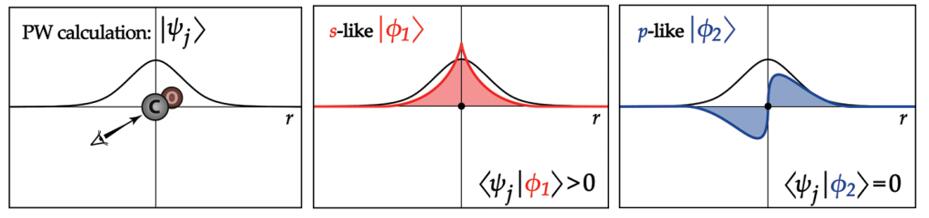
具体的方法就是把平面波的波函数近似的写成原子轨道线性组合的形式,k是k点,j是能带。
$$
\Phi_{j}(\mathbf{k}, \mathbf{r})=c_{j \mu}(\mathbf{k}) \phi_{\mu}(\mathbf{r})+c_{j \nu}(\mathbf{k}) \phi_{v}(\mathbf{r})+\ldots \approx \psi_{j}(\mathbf{k}, \mathbf{r})
$$
构建一个转换矩阵(transfer matrix),这个转换矩阵的矩阵元就近似的等于LCAO的系数。从而就可以构建投影密度矩阵,原本的哈密顿矩阵元就可以写成这个”转换矩阵”和能带能量相乘的形式。而后带回到原本的COHP公式里就可以得到适用于周期性体系的COHP方法。(具体看Dronskowski2011年文章)
Lobster
龙虾程序是Hoffmann的学生Richard Dronskowski教授开发的。
取名的原因是由于表示波函数的希腊字母ψ和龙虾很像。所以程序的图标也设计成了龙虾的样子。
程序主页:http://www.cohp.de/
目前最新版Lobster是3.1.0
支持Linux,windows,Mac OS X系统,一般我们计算完VASP会直接在服务器上处理COHP计算,所以用linux版即可。
Lobster程序和手册,常见问题都可以在官网上得到。不需要编译安装,可以直接使用。
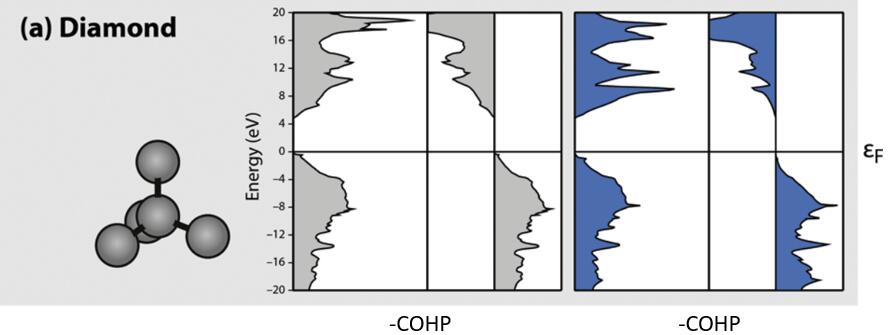
实例一:金刚石
由于,COHP在COOP的基础上引入了能量项,对于能量为负值的贡献是成键态,对于能量为正值的贡献是反键态,所以为了和COOP的计算结果看起来左右统一,一般在文章里看到的图都是 -COHP,即右边的峰是成键贡献,左边的峰是反键贡献。用LMTO和VASP算出来的结果非常接近,对于金刚石,所有的占据态都是成键成分,所有的反键态都是反键成分。
转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。