自洽计算的K点选取和 KPOINTS 文件生成

Jincheng Liu VASP KPOINTS

Created At : 2019-04-25 00:00

Views 👀 :

VASP的KPOINTS文件
KPOINTS文件形式
更方便的取K点的方法，VASPKIT
倒易空间与布里渊区
布里渊区

本文章为原创，版权归作者刘锦程所有，文章转载请先取得作者的同意，非常欢迎转发文章链接！严禁以任何方式挪用本文内容，用于以盈利为目的各种活动。

VASP的KPOINTS文件

在VASP 5.1.12以上版本中，KPOINTS文件可以缺省，k点信息写在INCAR里，但是不建议这么做：

一是因为INCAR里的K点只能设置每个K点之间的间距，不好直接指定K点的个数。二是数年来人们已经习惯了在KPOINTS里设定K点，一些VASP的插件有完善的生成KPOINTS的功能，用起来很方便。

在INCAR中设置K点是KGAMMA，和KSPACING这两个关键词，一般用不到，(因为用VASPKIT也可以做同样的事情)。KGAMMA是控制生成gamma中心K点，KSPACING是控制倒空间的K点和间隔距离，单位是Å-1

K点是VASP计算中的关键参数，一般计算要在第一布里渊区均匀撒点，能带计算在高对称点连线路径上取值。K点的密度由KPOINTS决定，KPOINTS取点越多，包含到计算里的信息越多，计算结果就要准确。VASP提供的自动取K点的方法有两种：

Monkhorst-Pack grids
Gamma centered Monkhorst-Pack grids

https://cms.mpi.univie.ac.at/vasp/vasp/Automatic_k_mesh_generation.html

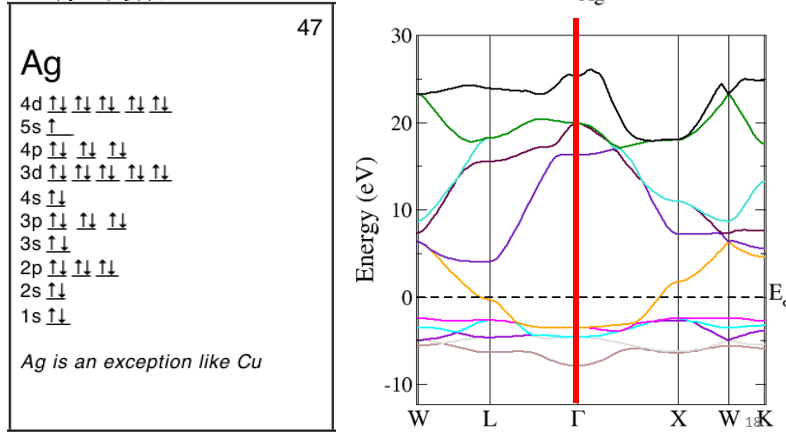
原子分子体系有孤立的确定的能级结构。而晶体在不同的k点上有不一样的能级结构。晶体在不同的方向上的势能是不一样的，且周期性无限重复。所以才有了band structure(能带图)，就是由一个一个的k点的能级信息拼接成的，比如$\Gamma$点计算得到的就是图中红线一条线上的数据，要计算其他k点的数据也要在其他的k点上解Kohn-Sham方程。

KPOINTS文件形式

Automatic mesh
0              ! number of k-points = 0 ->automatic generation scheme 
Gamma          ! generate a Gamma centered grid
4  4  4        ! subdivisions N_1, N_2 and N_3 along recipr. l. vectors
0. 0. 0.       ! optional shift of the mesh (s_1, s_2, s_3)

一共5行，需要改的只有第4行。

第一行，名字可以随便写，但是必须有

第二行，0代表VASP根据我们的要求自动产生K点

第三行，Gamma中心的Monkhorst-Pack grids

第四行，在倒格矢的三个方向上取K点的数目
1 1 1 # 1×1×1意思是在倒格矢a,b,c方向上都只取一个k点，一共1个k点
3 3 1 # 3×3×1意思是在倒格矢a,b方向上都取3个k点，c方向上取一个，一共9个
8 8 8 # 8×8×8，一共512个k点，

第五行，shift的值，Gamma center的K点就相当于MP方法shift了0.5 0.5 0.5

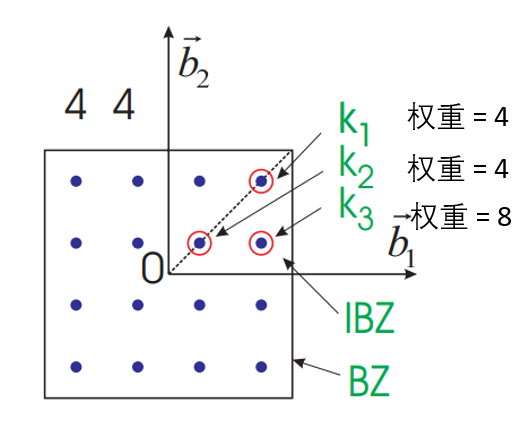
实际计算由于晶体的对称性会减除一大部分K点，比如算GaAs的primitive cell计算，在输出文件IBZKPT的第二行可以看到实际计算的K点数共29个。这些K点称为irreducible kpoints(不可约k点)。每个不可约K点的权重是相同对称性K点的个数。

KPOINTS的建议取值下图，每个晶格矢量的长度乘以这个方向上的k点数。注意要测试收敛性。

比如我要算一个绝缘体，a，b的晶胞长度为5 Å，c的长度为15 Å，则K点取 3 3 1。

d区金属，ka ~ 30 Å

普通金属，ka ~ 25 Å

半导体，ka ~ 20 Å

绝缘体，ka ~ 15 Å

以上建议是要严格遵守的嘛？不是！

读文献会发现，一些高水平文章诸如Science，Nature上仍然用着很糙，不精确的计算标准。一是因为计算机水平达不到，二是催化计算中我们关心的是相对能量，只要保持计算精度一样，往往可以误差抵消，定性勉强能用。

举例：对于正交的晶系(a=b=g= 90^o)用 POSCAR 中的晶格矢量，也就是下图中红框内的值，每一行代表一个基矢，取模，然后取倒数。这三个倒数的比值就是三个方向上k-points密度的取值。

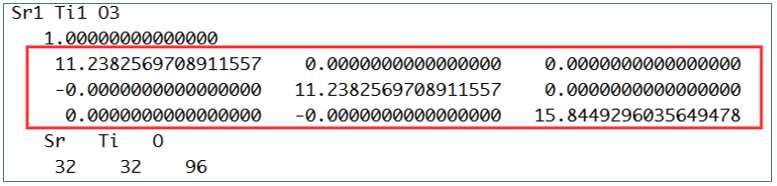$$ \frac{1}{11.238} : \frac{1}{11.238} : \frac{1}{15.845} \approx 1.4 : 1.4 : 1 $$

所以这个时候k-points有几种选择，
3 3 2,
4 4 3,
6 6 4,
7 7 5,

都是可以的，根据晶体的类型和所需要的计算精度选择。

更方便的取K点的方法，VASPKIT

我们只提前需要准备好一个POSCAR文件，运行

VASPKIT
1
102（产生自洽计算所用的KPOINTS文件功能）
2 （1:用MP方法；2:用Gamma中心的MP方法）
0.04 （倒格子中k点间距，单位是Angstrom-1，一般计算使用0.04，精确计算0.03或0.02）

这时候就自动生成KPOINTS了，还顺带生成了POTCAR和INCAR文件。比如：

K-Mesh Generated with KP-Resolved Value … : 0.030
0
Gamma
  12  12   1
0.0  0.0  0.0

再举个例子：

primitive cell的$\theta$-Al₂O₃，a = b = 6.14 Å ，c= 5.67 Å 。底心单斜。

这个非正交体系，倒格矢长度和实空间晶格常数不满足反比关系，所以要保证K点密度在各个方向长度相等，计算ka， kb， kc ~ ** 埃的规则在这里就不完全适用了。

这个时候最好的做法是用VASPKIT产生KPOINTS，在第一布里渊区均匀撒点，或者是在INCAR里设置KSPACING让vasp自己调整a，b，c方向上k-points密度。

Al4 O6
1.0
        6.1415114403         0.0000000000         0.0000000000
       -5.4373541295         2.8554058978         0.0000000000
       -1.3346698477         0.3291362294         5.5013695377
   Al    O
    4    6

a = 6.14151, b = 6.14151, c = 5.67052按照 ka~15埃的规则，算出来k点大约取3 3 3即可。但是用VASPKIT真正的算倒空间倒晶格矢量比例得到的推荐值是7 7 4。

注意事项：

该KPOINTS 文件里面,共有5行, # 或！后面为注释。
第三行,VASP只认第一个字母g, 大小写均可。也可以写成Gamma，Google。这是VASP关键词的一个特点，后面我们还会碰到好多关键词，只需要些首字母即可。
第四行，为生成对应数目的K点，建议使用VASPKIT生成。
第五行是，k点的shift值，一般不需要调，0 0 0即可。
对于原子或者分子的计算,K点取一个gamma点（1 1 1）就够了，多的K点是能提高周期性镜像分子间的相互作用精度，这部分能量是我们不想要的。即：对于含有真空层的体系，在真空层的方向上永远只使用一个K点。多余的K点只会增加真空层两边体系的相互作用的精度，而这一部分是我们不想要的。
Gamma点在VASP计算中非常重要,建议是,永远用gamma centered,也就是第三行保持G不变。比如ISMEAR=-5或者六方晶系只能用Gamma center的方法，不能用MP。（有文献报道对于计算孤立缺陷体系用MP方法，不包含Gamma点可以减少defect-defect interaction）
在文章计算说明部分应该给出所使用的k点数量，因为如果不这样做，就很难对这些结果再现。
增大超晶胞的体积减少了达到收敛时所需要的k点数量，因为实空间体积的增加对应于倒易空间体积的减少。只含有一个gamma点的计算可以使用vasp_gam版加速计算。
如果计算中涉及不同体积的超晶胞，并需要对其结果进行比较，则在倒易空间中选定k点时，需要使不同超晶胞倒易空间中的k点密度大体相同，这是使这些计算在k空间中具有类似的收敛精度的有效方法。说白了，a×ka ≈ b×kb ≈ c×kc，或者让VASPKIT均匀撒点。

倒易空间与布里渊区

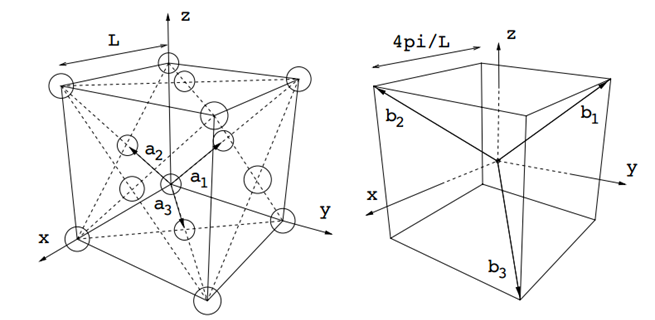
由此可见，在夹角一定的情况下，***a***₁和***b***₁的模成反比关系。（**也就是说在实空间某一个边很长的晶体，相应在该方向上取得K点数就应该越少；反之越多。**） unfold band

每个晶体结构都将由两套晶格与之相联系：一套是正晶格（或称正格子），另一套是倒晶格（或称倒格子）。第一性原理计算程序在做计算的时候通过傅里叶变换，在倒易空间中运算

一般解Kohn-Sham方程在倒空间完成，KS方程里并不是所有项都在倒易空间求解，电子动能和hartree势能更容易在倒空间算，交换相关能更容易在实空间算。VASP提供了一个选项可选赝势的非局域项在实空间投影还是倒空间投影（LREAL = .FALSE. 或者 Auto）。

布里渊区

布里渊区是倒格子空间中的 Wigner-Seitz primitive cell (维格纳塞茨原包)。第一布里渊区将中间格点和其所有相邻格点连接起来，在这些连线上做垂直平分面所围成的最小的体积。

二维体系的第一布里渊区例子：

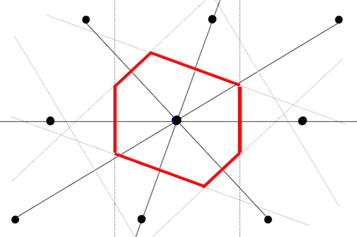
三维体系的第一布里渊区的例子：

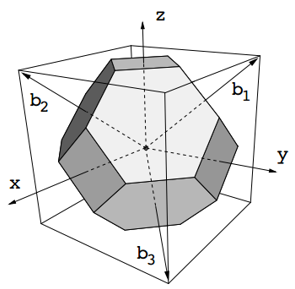
第一布里渊区包含了体系的所有性质，要精确求解体系的性质，需要在布里渊区中对倒空间简约波矢k做积分。

$$
\rho(\boldsymbol{r})=\frac{1}{\Omega_{\mathrm{BZ}}} \sum_{n} \int_{\mathrm{BZ}} f_{n \mathbf{k}}\left|\psi_{n \mathbf{k}}(\mathbf{r})\right|^{2} d \mathbf{k}
$$

但是，在倒易空间中不同的k点需要独立求解，所以，比较实际的做法就是在第一布里渊区均匀撒点，然后对不可约的k点做权重加和即可。

$$
\rho(\mathbf{r})=\sum_{n \mathbf{k}} w_{\mathbf{k}} f_{n \mathbf{k}}\left|\psi_{n \mathbf{k}}(\mathbf{r})\right|^{2} d \mathbf{k}
$$

VASP中所谓的取k点(KPOINTS)，就是指这一过程。显然，k点取得越密，包含的倒易空间中的信息就越多，结果也越精确。

转载请注明来源，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达。