本文章为原创,版权归作者刘锦程所有,文章转载请先取得作者的同意,非常欢迎转发文章链接!严禁以任何方式挪用本文内容,用于以盈利为目的各种活动。
一句话提要:孤立分子体系没有能带的概念,只有能级的概念。而周期性体系在倒易空间中不同的k点的能级时不一样的,从而产生能带。本文讨论能带的成因,轨道作用的方式、强弱、维度对能带结构的影响。
相关内容:
当原子形成分子时,原子轨道之间发生相互作用会产生具有孤立能级的分子轨道。比如两个氢原子靠近的时候,两个1s轨道线性组合生成一个成键轨道和一个反键轨道。
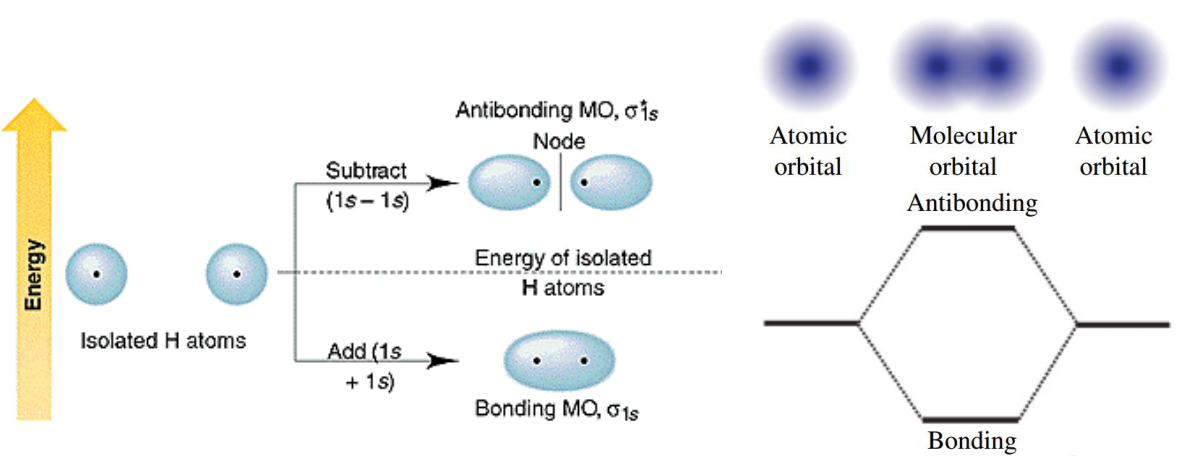
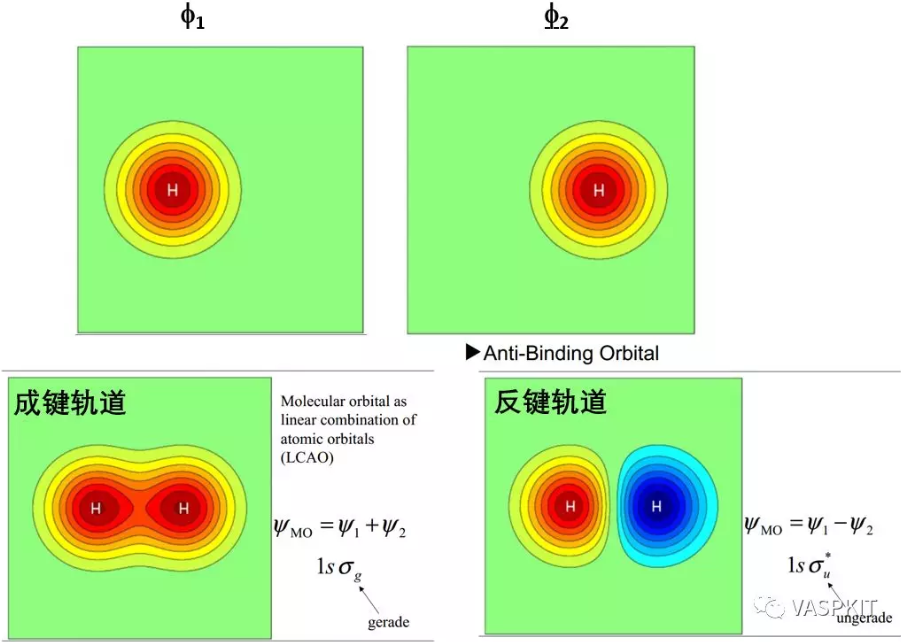
对于晶体是周期性系统,如果有无限个氢原子形成一维氢原子链,则会形成连续的能级。
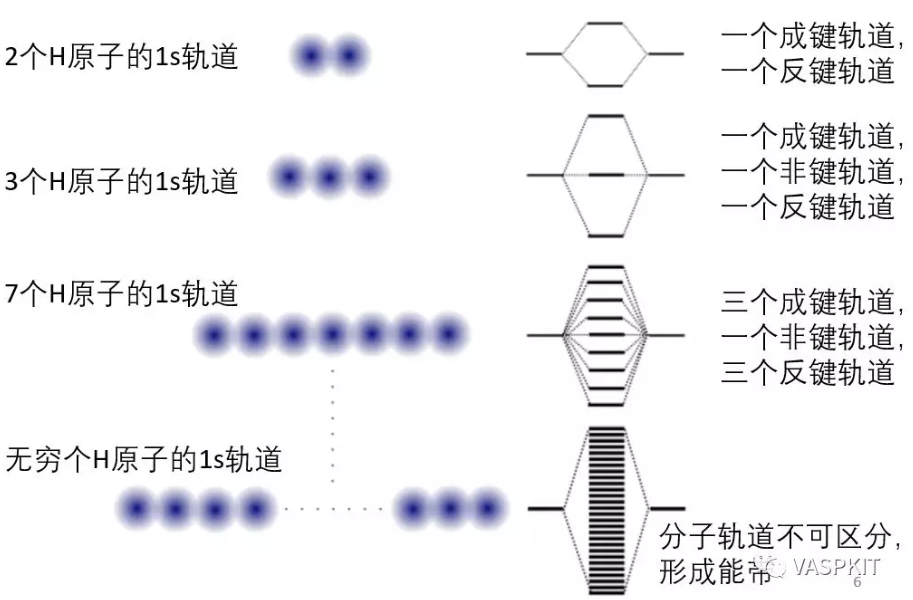
对于等距的一维的H原子链,用紧束缚模型,根据bloch定理可以把波函数写为原子轨道的线性组合的形式,展开系数是和倒易空间波矢k有关的e指数形式,k的取值范围在[-π/a, π/a]之间,其中a是实空间H原子间距。
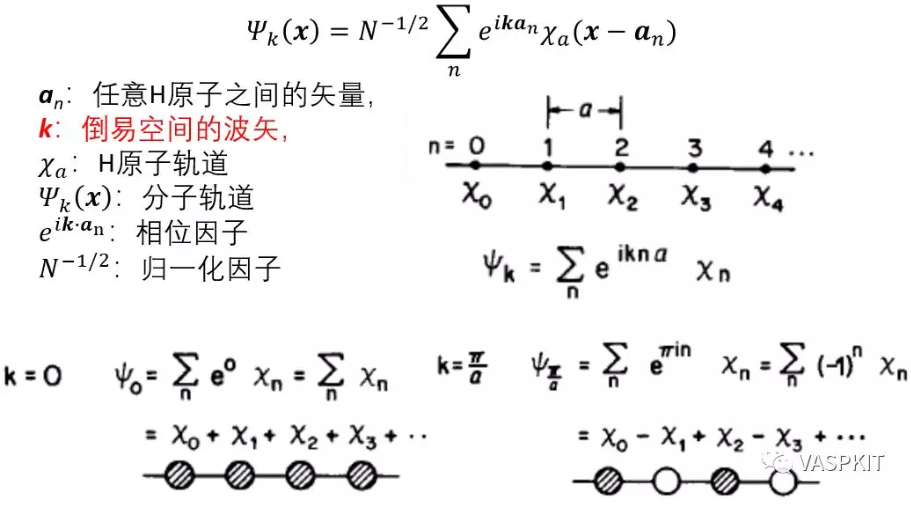
倒易空间波矢k直接决定了展开系数,从而决定了波函数的形式。
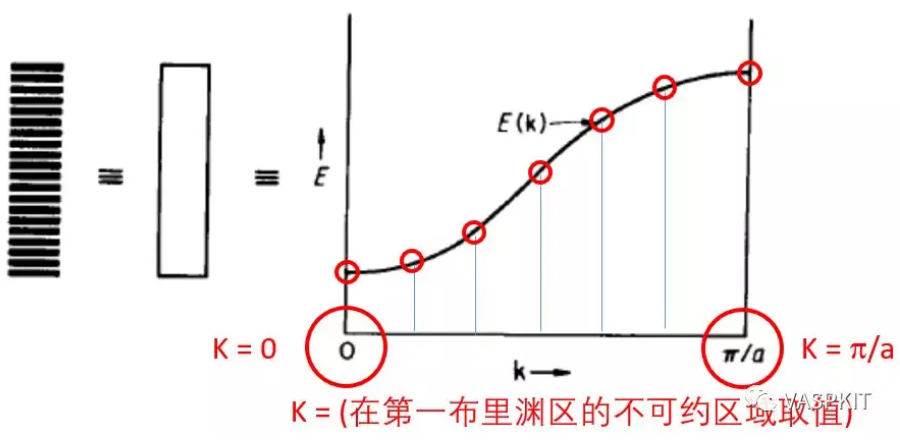
对于一维氢原子链,k取0时,e0=1,即所有H原子轨道的展开系数都是1,此时生成的轨道(能带)能量最低;k取π/a时,einπ导致n取不同数值时,相邻的H原子轨道系数是相反的,此时生成的轨道(能带)能量最高。如果k取在[0, π/a]之间时,可以证明同一条能带能量一定是连续变化的。这样如果在[0, π/a]间隔取一系列的k值,计算其能量,则连成一条曲线,就是最简单的一维H原子链1s轨道形成的能带。纵坐标是轨道/能带能量 (eV),横坐标是k取值路径的倒空间距离,一般叫做k-path,单位是 Angstrom-1。
如果我们讨论二维体系,那么k点的取值就是两个数字的组合了kx和ky。对于二维正方形体系的布里渊区,其中一些特殊点(高对称点)有特殊的符号,比如:$\Gamma$(kx=0, ky=0), X(kx=π/a, ky=0), M(kx=π/a, ky=π/a), 所谓的做算能带结构,就是算这些高对称点上的连线上的能级结构(即:不可约布里渊区的边界)。这样我们计算二维材料s和p原子轨道的相互作用。简单的算出$\Gamma$, X, M 这三个点的能级排布,然后连线,就得到了最简单的能带结构图。
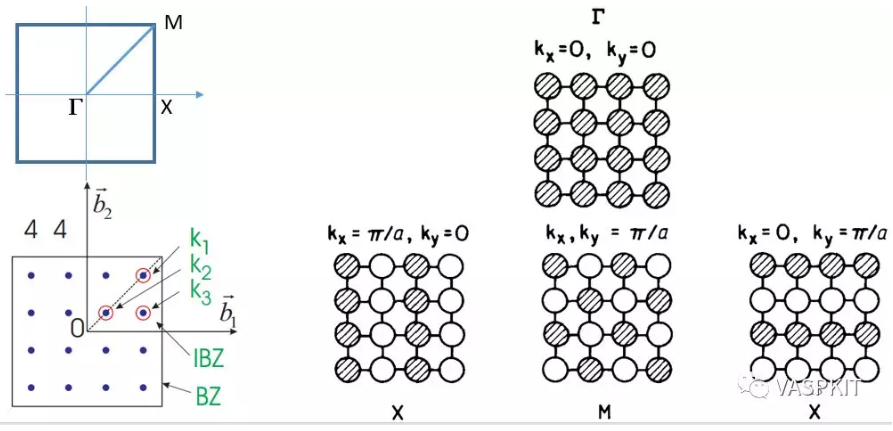
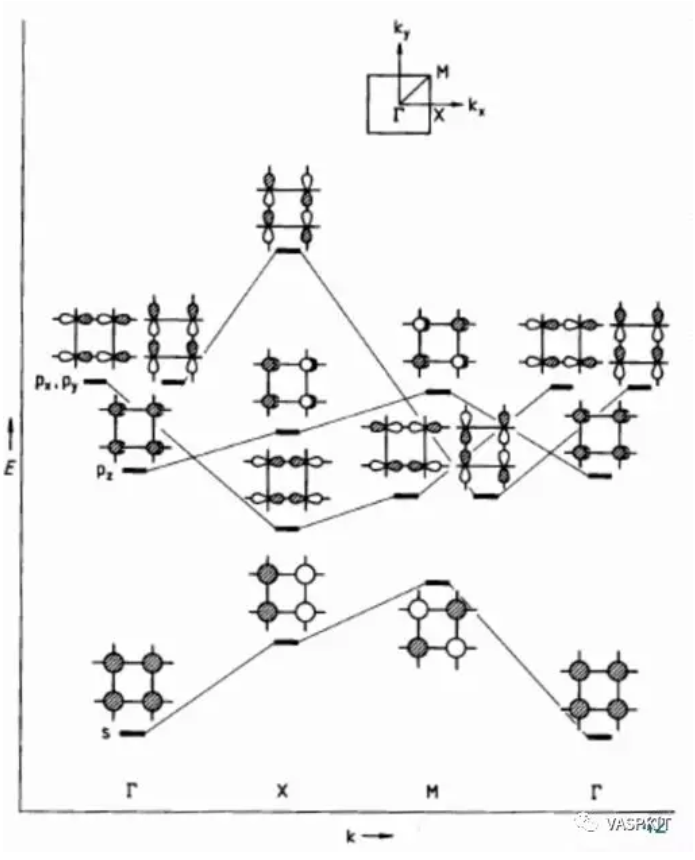
二维材料的布里渊区种类比较少,列举如下,而三维材料的布里渊区的形状和种类比较复杂(Computational Materials Science 128 (2017) 140–184. 这篇文章讨论了所有的三维材料的布里渊区和K-path取法)。
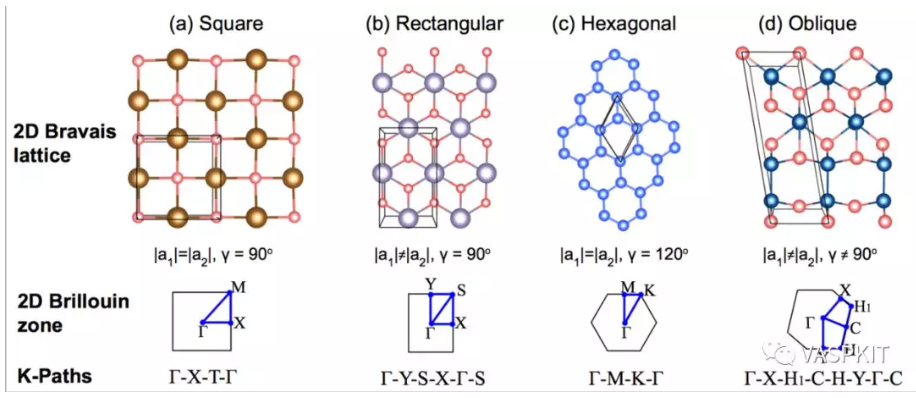
那么能带的走势有什么规律吗?有的,而且很重要。一条能带的宽度通常指的是这条能带的所覆盖的能量范围。能带宽度主要由原子轨道的重叠大小和相互作用强弱决定,是有方向性的。我们还是回到H2分子的情况。当两个氢原子距离远的时候,成键和反键轨道的能量差小,当两个氢原子距离近的时候,成键和反键轨道的能量差大。
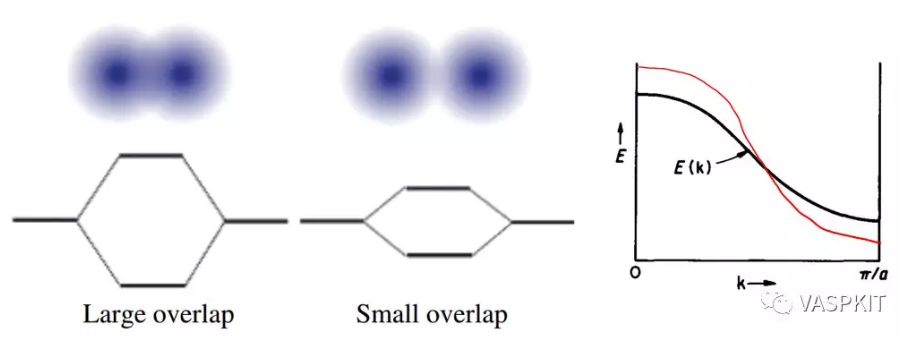
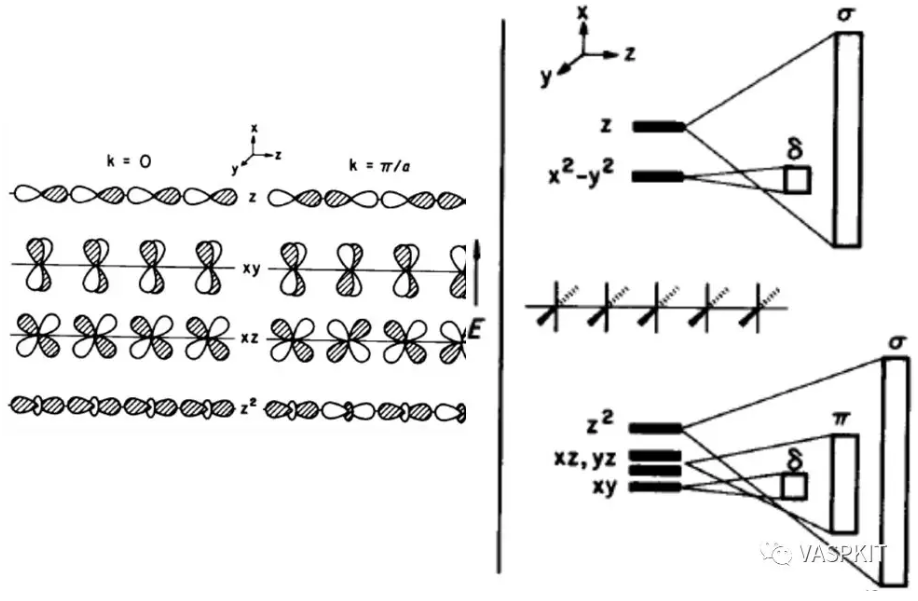
实际上组成分子轨道的原子轨道不止1s轨道一个,所以组成的分子轨道也很多,不同的原子轨道组合会出现好多能带。由于成键方式不一样,能带的走势也会不一样。比如对于一维K2PtH4链,Pt的d轨道就有$\sigma$,$\pi$,$\delta$这三种键。
头碰头形式的$\sigma$键的相互作用最强,能级分裂大,能带覆盖的能量范围也就越大,形状上也就约陡峭。
肩并肩形式或背靠背的$\pi$键$\delta$键的相互作用稍弱,能带就稍微平缓。
局域性质很强的轨道比如镧系元素的f轨道,几乎不和相邻原子成键,能带就基本是平的。
做半导体计算一项重要内容是有效质量计算,在VBM和CBM位置如果能带陡峭(即能量对k二阶导数大),这就是个有效质量小的材料,表现出更好的载流子迁移性质。
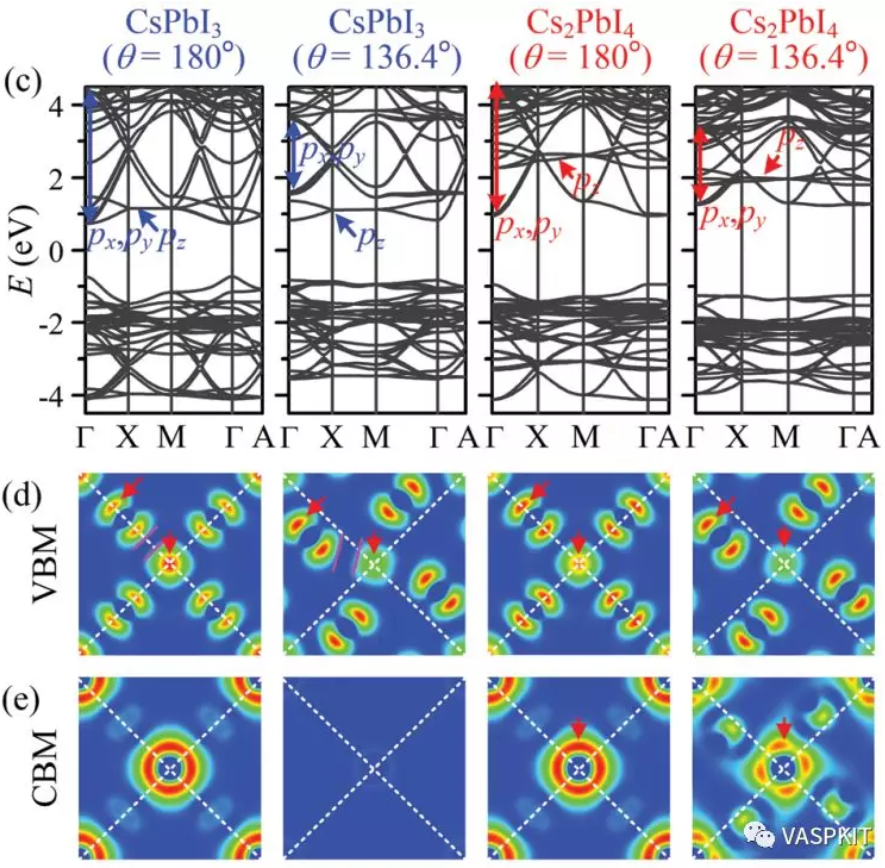
除了能带的走势,对比具有相同角动量贡献的能带可以对材料的各向异性有更深入的分析,例如:如果材料的px,py,pz的能带走势很不同,那么此材料在x、y、z三个方向表现出来的电子结构性质就很可能不同,下面这篇文章研究CsxPdIy材料提出的电子维度的概念(electronic dimensionality)也是在能带结构上做了此类的分析。对于这样的三维材料,不是在所有方向都导电的,而是在某些方向上导电,某些方向上绝缘。
转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。