基于能量-应变关系计算弹性常数—VASPKIT v1.00新功能

Jincheng Liu VASPKIT 弹性

Created At : 2019-08-18 00:00

Views 👀 :

本文原作者Wang Vei，版权归作者王伟所有，文章转载请先取得作者的同意，非常欢迎转发文章链接！严禁以任何方式挪用本文内容，用于以盈利为目的各种活动。

一句话提要：VASPKIT v1.00可以批量生成施加应变以后的结构，并根据能量-应变关系求解弹性常数矩阵。

相关内容：

计算能带反折叠—VASPKIT v1.00新功能

计算跃迁电偶极矩—VASPKIT v1.00新功能

深入分析能带结构(二)-VASPKIT能带图计算

VASPKIT计算电荷密度差 http://blog.wangruixing.cn/2019/05/19/pymatgen-band/)

在材料的线性形变范围内（应变较小的情况下），体系的应力与应变满足胡克定律，
$$
\sigma_{i}=\sum_{j=1}^{6} c_{i j} \varepsilon_{j}
$$
其中$\sigma_{i}$和$\boldsymbol{\varepsilon}_{i}$分别表示应力和应变，$C_{i j}$是弹性刚度常数，这里$1 \leq i \leq 6$，即应变和应力分别有6个独立分量。

施加应变后体系的应变能$\Delta E\left(V,\left{\varepsilon_{i}\right}\right)$可按应变张量$\boldsymbol{\varepsilon}_{i}$进行泰勒级数展开并取二阶近似得到：

$$
\Delta E\left(V,\left{\varepsilon_{i}\right}\right)=E\left(V,\left{\varepsilon_{i}\right}\right)-E\left(V_{0}, 0\right)=\frac{V_{0}}{2} \sum_{i, j=1}^{6} C_{i j} \varepsilon_{j} \varepsilon_{i}
$$

这里$E\left(V,\left{\varepsilon_{i}\right}\right)$和$E\left(V_{0}, 0\right)$分别表示施加应变后和基态构型的总能，$V_{0}$是平衡体积。

因此，采用第一性原理计算弹性常数有两种方法，第一种方法是应力-应变方法，即通过给结构施加不同应变，分别计算出所对应的应力大小，然后利用公式（1）拟合得到一次项系数，从而得到$C_{i j}$。第二种方法是能量-应变方法，即通过给结构施加不同应变后计算出体系总能相对于基态能量变化（应变能），再利用公式（2）进行二次多项式拟合，其中二次多项式系数是晶体的某个弹性常数或者弹性常数组合。第一种方法优点是每进行一次计算可一次得到$\sigma_{i}
$六个独立分量，缺点是为了得到准确的应力大小，必须选择更高的截断能和更密集的K格点。在同样的精度下，能量-应变法相比应力-应变方法要求的截断能和K点数目相对较少，缺点是计算应变数目有所增加。VASPKIT中弹性常数计算基于能量-应变法，目前不支持三斜晶系。

###VASP+VASPKIT基于能量-应变法计算晶体弹性常数及力学性质

这里我们以金刚石结构为例讲解如何采用能量-应变函数关系计算弹性常数，详见VASPKIT/examples/elastic/diamond_3D。对于金刚石立方结构，一共有3个独立弹性常数，$\mathrm{C}_{11}, \mathrm{C}_{12}$,和 $\mathrm{C}_{44}$。

立方晶系的弹性能可以表示
$$
\Delta E\left(V,\left{\varepsilon_{i}\right}\right)=\frac{V_{0}}{2}\left[\begin{array}{cccccc}
\varepsilon_{1} & \varepsilon_{2} & \varepsilon_{3} & \varepsilon_{4} & \varepsilon_{5} & \varepsilon_{6}\end{array}\right]\left[ \begin{array}{cccccc}{C_{11}} & {C_{12}} & {C_{12}} & {0} & {0} & {0} \\ {C_{12}} & {C_{11}} & {C_{12}} & {0} & {0} & {0} \\ {C_{12}} & {C_{12}} & {C_{11}} & {0} & {0} & {0} \\ {0} & {0} & {0} & {C_{44}} & {0} & {0} \\ {0} & {0} & {0} & {0} & {C_{44}} & {0} \\ {0} & {0} & {0} & {0} & {0} & {C_{44}}\end{array}\right]
\left[ \begin{array}{l}{\varepsilon_{1}} \\ {\varepsilon_{2}} \\ {\varepsilon_{3}} \\ {\varepsilon_{4}} \\ {\varepsilon_{5}} \\ {\varepsilon_{6}}\end{array}\right]
$$
设定$\varepsilon=(0,0,0, \delta, \delta, \delta)$，可得$\Delta E=\frac{V_0}{2}\left(C_{44} \varepsilon_{4} \varepsilon_{4}+C_{44} \varepsilon_{5} \varepsilon_{5}+C_{44} \varepsilon_{6} \varepsilon_{6}\right)$，因此有$\frac{\Delta E}{V_0}=\frac{3}{2} C_{44} \delta^{2}$ [1]。

设定$\varepsilon=(\delta, \delta, 0,0,0,0)$，可得$\Delta E=\frac{V}{2}\left(C_{11} \varepsilon_{1} \varepsilon_{1}+C_{11} \varepsilon_{2} \varepsilon_{2}+C_{12} \varepsilon_{1} \varepsilon_{2}+C_{12} \varepsilon_{2} \varepsilon_{1}\right)$，因此有$\frac{\Delta E}{V_0}=\left(C_{11}+C_{12}\right) \delta^{2}$

再设定$=(\delta, \delta, \delta, 0,0,0)
$，可得$\frac{\Delta E}{V_0}=\frac{3}{2}\left(C_{11}+2 C_{12}\right) \delta^{2}$。

联立以上三个方程组，即可得到三个独立弹性常数。

施加形变后的晶格基矢可通过下式得到 [2]:
$$
\left( \begin{array}{l}{\boldsymbol{a}^{\prime}} \\ {\boldsymbol{b}^{\prime}} \\ {\boldsymbol{c}^{\prime}}\end{array}\right)=\left( \begin{array}{l}{\boldsymbol{a}} \\ {\boldsymbol{b}} \\ {\boldsymbol{c}}\end{array}\right) \cdot(\boldsymbol{I}+\boldsymbol{\varepsilon})
$$
其中$\boldsymbol{I}$是单位矩阵，
$$
\boldsymbol{\varepsilon}=\left( \begin{array}{ccc}{\varepsilon_{1}} & {\frac{\varepsilon_{6}}{2}} & {\frac{\varepsilon_{5}}{2}} \\ {\frac{\varepsilon_{6}}{2}} & {\varepsilon_{2}} & {\frac{\varepsilon_{4}}{2}} \\ {\frac{\varepsilon_{5}}{2}} & {\frac{\varepsilon_{4}}{2}} & {\varepsilon_{3}}\end{array}\right)
$$
VASPKIT和VASP计算晶体的弹性常数具体计算步骤分为：

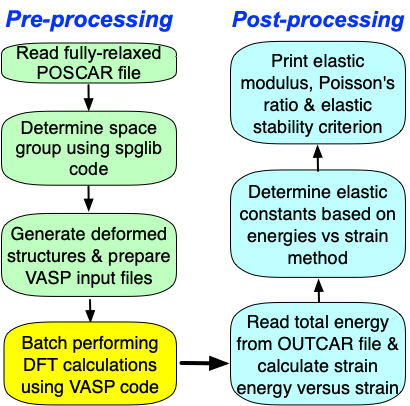
1，准备优化彻底的POSCAR文件，注意通常采用标准的惯用原胞计算弹性常数，如果不确信POSCAR文件中是否是标准的惯用原胞，可以用VASPKIT-603/604生成标准结构；

2，运行VASPKIT 选择102生成KPOINTS，由于计算弹性常数对K-mesh要求很高，因此对于半导体（金属体）体系，生成K点的精度应不小于$0.03(0.02) \times 2 \pi $ $ {\AA}^{-1}$

3，INCAR参考设置如下；

Global Parameters
  ISTART =  0        
  LREAL  =  F      
  PREC   =  High  （截断能设置默认值1.5-2倍）
  LWAVE  = F       
  LCHARG = F     
  ADDGRID= .TRUE.    
Electronic Relaxation
  ISMEAR =  0          
  SIGMA  =  0.05       
  NELM   =  40           
  NELMIN =  4           
  EDIFF  =  1E-08       
Ionic Relaxation
  NELMIN =  6          
  NSW    =  100         
  IBRION =  2           
  ISIF   =  2    （切记选择2,如果选择3会把施加应变后原胞重新优化成平衡原胞）
  EDIFFG = -1E-02

4，准备VPKIT.in文件并设置第一行为1（预处理）；运行VASPKIT并选择201, 将生成用于计算弹性常数文件；

1                    ! 设置1将产生计算弹性常数的输入文件，2则计算弹性常数
3D                   ! 2D为二维体系，3D为三维体系
7                    ! 7个应变
-0.015 -0.010 -0.005 0.000 0.005 0.010 0.015  ! 应变变化范围

运行VASPKIT后输出一下信息

 ------------>>
201
  -->> (01) Reading VPKIT.in File...
 +-------------------------- Warm Tips --------------------------+
      See an example in VASPKIT/examples/elastic/diamond_3D,
   Require the fully-relaxed and standardized Convertional cell.
 +---------------------------------------------------------------+
  -->> (02) Reading Structural Parameters from POSCAR File...
   -> C44 folder created successfully!
   -> strain_-0.015 folder created successfully!
   -> strain_-0.010 folder created successfully!
   -> strain_-0.005 folder created successfully!
   -> strain_0.000 folder created successfully!
   -> strain_+0.005 folder created successfully!
   -> strain_+0.010 folder created successfully!
   -> strain_+0.015 folder created successfully!
   -> C11_C12_I folder created successfully!
   -> strain_-0.015 folder created successfully!
   -> strain_-0.010 folder created successfully!
   -> strain_-0.005 folder created successfully!
   -> strain_0.000 folder created successfully!
   -> strain_+0.005 folder created successfully!
   -> strain_+0.010 folder created successfully!
   -> strain_+0.015 folder created successfully!
   -> C11_C12_II folder created successfully!
   -> strain_-0.015 folder created successfully!
   -> strain_-0.010 folder created successfully!
   -> strain_-0.005 folder created successfully!
   -> strain_0.000 folder created successfully!
   -> strain_+0.005 folder created successfully!
   -> strain_+0.010 folder created successfully!
   -> strain_+0.015 folder created successfully!

5，批量提交vasp作业；

6，再次修改VPKIT.in文件中第一行为2（后处理），然后再次运行VASPKIT并选择201，得到以下结果；

 ------------>>
201
  -->> (01) Reading VPKIT.in File...
 +-------------------------- Warm Tips --------------------------+
      See an example in VASPKIT/examples/elastic/diamond_3D,
   Require the fully-relaxed and standardized Convertional cell.
 +---------------------------------------------------------------+
  -->> (02) Reading Structural Parameters from POSCAR File...
  -->> (03) Calculating the fitting coefficients of energy vs strain.
 -->> Current directory: Fitting Precision
                    C44:  0.817E-09
              C11_C12_I:  0.814E-08
             C11_C12_II:  0.135E-07
 +-------------------------- Summary ----------------------------+
 Based on the Strain versus Energy method.
 Crystal Class: m-3m
 Space Group: Fd-3m
 Crystal System: Cubic system
 Including Point group classes: 23, 2/m-3, 432, -43m, 4/m-32/m
 There are 3 independent elastic constants
    C11  C12  C12    0    0    0
    C12  C11  C12    0    0    0
    C12  C12  C11    0    0    0
      0    0    0  C44    0    0
      0    0    0    0  C44    0
      0    0    0    0    0  C44

 Stiffness Tensor C_ij (in GPa):
   1050.640    126.640    126.640      0.000      0.000      0.000
    126.640   1050.640    126.640      0.000      0.000      0.000
    126.640    126.640   1050.640      0.000      0.000      0.000
      0.000      0.000      0.000    559.861      0.000      0.000
      0.000      0.000      0.000      0.000    559.861      0.000
      0.000      0.000      0.000      0.000      0.000    559.861

 Compliance Tensor S_ij (in GPa^{-1}):
   0.000977  -0.000105  -0.000105   0.000000   0.000000   0.000000
  -0.000105   0.000977  -0.000105   0.000000   0.000000   0.000000
  -0.000105  -0.000105   0.000977   0.000000   0.000000   0.000000
   0.000000   0.000000   0.000000   0.001786   0.000000   0.000000
   0.000000   0.000000   0.000000   0.000000   0.001786   0.000000
   0.000000   0.000000   0.000000   0.000000   0.000000   0.001786

 Elastic stability criteria as discussed in PRB 90, 224104 (2014):
 Criteria (i) C11 - C12 > 0 meeted.
 Criteria (ii) C11 + 2C12 > 0 meeted.
 Criteria (iii) C44 > 0 meeted.

 Average mechanical properties for polycrystalline:
 +---------------------------------------------------------------+
 |        Scheme             |   Voigt   |   Reuss   |    Hill   |
 +---------------------------------------------------------------+
 |  Bulk modulus K (GPa)     |  434.640  |  434.640  |  434.640  |
 |  Shear modulus G (GPa)    |  520.716  |  516.130  |  518.423  |
 |  Young's modulus E (GPa)  | 1116.342  | 1109.298  | 1112.824  |
 |  P-wave modulus (GPa)     | 1128.929  | 1122.814  | 1125.871  |
 |  Poisson's ratio v        |    0.072  |    0.075  |    0.073  |
 |  Bulk/Shear ratio         |    0.835  |    0.842  |    0.838  |
 +---------------------------------------------------------------+
 Pugh Ratio: 1.193
 Cauchy Pressure (GPa): -433.220
 Universal Elastic Anisotropy: 0.044
 Chung–Buessem Anisotropy:    0.004
 Isotropic Poisson’s Ratio: 0.073
 Longitudinal wave velocity (in m/s):  17945.173
 Transverse wave velocity (in m/s):  12177.146
 Average wave velocity (in m/s):  13280.911
 Debye temperature (in K): 2212.889
 References:
 [1] Voigt W, Lehrbuch der Kristallphysik (1928)
 [2] Reuss A, Z. Angew. Math. Mech. 9 49–58 (1929)
 [3] Hill R, Proc. Phys. Soc. A 65 349–54 (1952)
 [4] Debye temperature J. Phys. Chem. Solids 24, 909-917 (1963)
 [5] Elastic wave velocities calculated using Navier's equation

金刚石弹性常数实验值分别为：$C_{11}=1079$ GPa, $C_{12}=124$ GPa和$C_{44}=578$ GPa [3],通过比较发现采用VASPKIT结合VASP得到的理论计算弹性常数与实验值符合较好。另外，最新版本也支持从OUTCAR或ELASTIC_TENSOR.in文件中读取弹性常数，计算各种力学性质，见VASPKIT/examples/elastic。

参考文献：

[1] 武松，利用 VASP 计算不同晶系晶体弹性常数

[2] 侯柱锋，采用VASP如何计算晶体的弹性常数

[3] McSkimin H J and Andreatch P 1972 J. Appl. Phys. 43 2944

转载请注明来源，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达。