原作者无缺,本文经原作者同意转载。出自“学术之友”。
准备写一份使用 VASP 计算磁性材料的个人经验小结,计划分为三个部分:加快磁性材料电子迭代收敛经验小结、磁性材料声子谱计算经验小结、磁性材料 HSE06 能带计算经验小结。
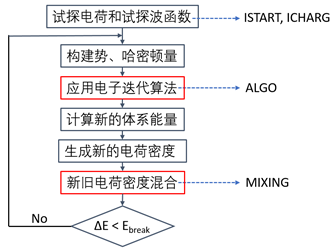
上图为 VASP 进行电子自洽迭代的简要流程,详细流程图可查阅 VASP 手册 Theoretical Background 的说明。在整个自洽迭代过程中,迭代收敛阈值(EIDFF 参数)设置好以后,我们可以干预的主要有三个地方:
1) 如何构建初始电荷及试探波函数(由 ISTART 和 ICHARG 参数控制):常见的有两种做法,由 VASP 自己生成一个试探波函数或者使用其他计算的波函数作为本次计算的初始波函数;
2) 电子迭代算符 (ALGO)的选择:可以使用 ALGO 或 IALGO 参数设置所使用的电子迭代算法。其中使用 ALGO 进行设置会更加方便,手册上明确建议使用 ALGO,无法使用 ALGO 设置的迭代算法可能会不稳定。个人常用 ALGO = Normal 和 ALGO = Fast。此外某些情况下 Damped 或 All 也是比较好的选择;
3) 新旧电荷密度如何混合(MIXING):VASP 在电子迭代过程中,不会把生成的新的电荷密度直接作为下一步迭代的输入电荷密度,而是先混入一部分的旧的电荷密度得到混合的电荷密度, 再输入到下一步迭代。这里就会涉及到两个问题:新旧电荷密度的混合方式以及旧电荷密度的混入比例。混合方式和混合比例都可以通过 INCAR 中的参数进行控制。对于磁性材料,选择好的 MIXING 可以使得计算快速收敛,见后文的说明及测试例子。
ALGO 的一些说明
以下是个人整理的 ALGO 参数使用简要说明及注意事项,详细说明可翻阅 VASP 手册。
1、ALGO = Normal (默认值)
1) 即 IALGO = 38,稳定性最好(手册原文:Please mind, that the RMM-DIIS algorithm can fail in rare cases, whereas IALGO = 38 did not fail for any system tested up to date.)。
2) 使用这一算法出现问题时,可尝试降低 NSIM。
2、ALGO = Very_Fast
1) 即 IALGO = 48,电子步耗时要比 ALGO = Normal 少得多(至少对于大体系以及小内存带宽的工作站来说是如此)。说对于容易收敛(比如体系无磁性或磁性结构很简单)的大体系,可以考虑使用 ALGO = Very_Fast;
2) 可靠性较 ALGO = Normal 差,少数情况下使用 ALGO = Very_Fast 会失败,此时建议换成 ALGO = Normal;
3) 一般来说,使用这一算法主要会遇到两个问题:首先是 MD 和弛豫时未占据带的优化可能会失败,这一问题可以在 INCAR 中加入 WEIMIN = 0 解决;
4) 另外一个问题是轨道初始化不合理时,这一迭代算法可能无法正确收敛:增加 NBANDS可以有效改善这一问题,若依然无法收敛,建议使用 ALGO = Fast;
5) 无法收敛时,可尝试降低 AMIX,增加 BMIX。
3、ALGO = Fast
1) 使用两种电子迭代算法:在自洽迭代开始几步,VASP 会先使用 IALGO = 38 进行迭代,以获得相对合理的初始电荷密度(以避免出现上面提到的 ALGO = Very_Fast 会遇到的第二个问题),后面再换成 IALGO = 48。对于结构优化,在第一步离子步之后,每一步离子步都会先执行一步 IALGO = 38,然后再换成 IALGO = 48;
2) 这种方法相当可靠;
3) 后面会切换成 IALGO = 48 后,电子步耗时会比 IALGO = 38 短。因此在相同电子迭代步数前提下,使用 ALGO = Fast 耗时会短于 ALGO = Normal。
4、ALGO = Damped
1) 即 IALGO = 53;
2) 对于小带隙体系和金属,常需要更大的 NBANDS,此时可考虑使用 ALGO = Damped;
3) 对于小带隙体系和金属,结合 LDIAG = .TRUE.,可以有效计算这些体系的基态;若使用 LDIAG = .FLASE.,收敛会更快,但是计算可靠性会显著下降;
4) TIME 的设置非常重要。太小的 TIME 值会导致收敛显著变慢,太大则会导致迭代不收敛。建议优化 TIME 值(特别是体系具有许多不同的组态时):从小的 TIME 开始测试,逐步增加 1.2 倍直至计算发散,然后取计算稳定收敛下最大的 TIME 值,将其用于所有的计算中。这一优化过程可以使用脚本批量测试。
5、ALGO = All
1) 即 IALGO = 58;
2) 建议用于绝缘体。对于非自旋极化体系,这一迭代算法通常在能带数目等于电子数一半时具有最佳稳定性(此时这一算法相当可靠,甚至可能优于混合算法,即 ALGO = Fast);
3) TIME 的设置非常重要。参见 ALGO = Damped 中的说明。
6、选择迭代算法时需要考虑的因素:
1) 对耗时和稳定性的平衡,其中耗时又具体表现在单步电子步耗时和电子迭代步数上:上述迭代算法,比如 ALGO = Normal,收敛稳定性好,一般来说所用的迭代步数较少,但是单步电子步耗时较长(当然可以通过堆计算核心降低单步电子步耗时),对于小体系计算是很好的选择。而 ALGO = Fast,大部分迭代使用的 IALGO = 48 算法,单步电子步耗时短,用于结构简单的大体系时,自洽计算耗时可能会比 ALGO = Normal 要有优势;但是体系结构复杂或者状态复杂(比如磁性体系)时,ALGO = Fast 可能会收敛困难甚至不收敛。对计算耗时有较高要求的话,在确定好体系是金属还是半导体后,可以考虑 ALGO = Damped + TIME + LDIAG 或者 ALGO = All + TIME 组合;
2) 体系基态是金属还是半导体,若是半导体,带隙大小如何:这不仅会影响 ALGO 的选择(All 和 Damped 哪个更适合),对于磁性体系还会影响 MIXING 参数的设置(见下文)。如何快速判断体系是半导体还是金属见下文说明;
3) 体系是否具有磁性:复杂磁性体系常常会遇到难以收敛的问题。我自己会把收敛稳定性放在更重要的位置,计算耗时就通过堆计算核心去降低。
如何快速判断体系是半导体还是金属
我个人通常习惯做分步结构优化。在第一步结构优化中,使用较低精度,同时设置 ISMEAR = 0 + SIGMA = 0.1,查看结构优化最后在 OUTCAR 中给出的 EENTRO 值。然后通过 EENTRO 值除以体系原子数去判断体系是半导体和金属:
1) ( EENTRO / 原子数 ) 大于 1meV,体系为金属。
2) ( EENTRO / 原子数 ) 小于 0.1meV,体系为半导体。这个值非常小时,比如 0.000001,体系带隙一般较大。
3) ( EENTRO / 原子数 ) 介于 1meV 和 0.1meV,目前还没有具体测试过,不确定。
这一判断的依据是:对于金属体系,ISMAER = 0 会使用 Gaussian smearing,导致在费米面处出现分数占据,进而导致 EENTRO 值不为 0 。而对于较大带隙的半导体,SIGMA = 0.1 还无法导致费米面处出现分数占据,EENTRO 值保持为 0(若增大 SIGMA 到一个很大的值时,EENTRO 也将不再保持为 0,但此时的计算会存在问题)。
这一判断方法是我个人的经验,目前在使用过程中大部分情况下都能给出正确的结果,但不保证对所有体系所有情况都可用。比如在弛豫过程中晶格变化非常大时,用于自洽计算对应的平面波截断球已经严重变形,可能会导致离子步的自洽收敛到的状态本身就有很大的误差。此时再在有误差的自洽结果上用这一方法进行判断是否可行,我不确定。不过解决办法也简单,再用弛豫的结构做一次弛豫就可以使用这一方法进行判断了。
MIXING 参数的一些说明
在 VASP 中可以控制新旧电荷密度混合方式以及旧电荷密度混入比例。对于磁性材料,调节 MIXING 参数不仅可以有效减少迭代步数,还可以使得体系收敛到更低的磁态上。相关参数简要说明如下:
1、IMIX:新旧电荷密度混合方式
1) IMIX = 1
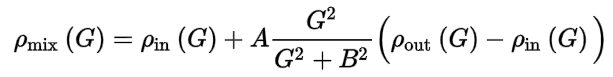
A = AMIX, B = BMIX.
- 使用 Kerker 混合方法,具体 ρ(out) 和 ρ(in) 分别为新旧电荷密度。
- 这一方法较少使用。目前我仅看到在 vasp 论坛上管理员建议在进行 HSE06 计算,选择 ALGO = Normal 时,使用 IMIX = 1。
2) IMIX = 4 (默认值)
当参数 WC > 0 时,使用 Pulay’s scheme,WC = 0 时选择 Broyden’s 2nd method。其中默认值为 WC > 0。目前 Pulay’s sheme 总是好于 Broyden’s 2nd method。不建议修改 WC 参数。
需要说明的是,VASP 默认使用 WC > 0,此时在 OUTCAR 中说明使用的是 modified Broyden-mixing sheme。可能这一方法就是 Pulay’s sheme。
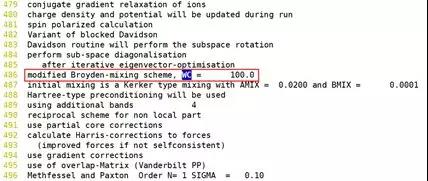
此时 AMIX 参数的设置非常依赖于体系。见下面的说明。
2、BMIX:Kerker 混合方法截断波矢量
1) 对于 slab、磁性体系和绝缘体(例如分子和团簇),使用 BMIX = 0.0001 + BMIX_MAG = 0.0001(即 “线性混合” ),可以使得电子迭代更快收敛;
2) 使用 “线性混合“ 时,AMIX 的设置非常关键。
3、AMIX:线性混合参数。在 IMIX = 4 时:
1) AMIX 参数的设置非常依赖于体系:对于金属体系,AMIX 通常相当小(AMIX = 0.02)。而对于半导体体系,从我目前的测试结果来看,使用 AMIX = 0.2 大部分情况下可以使得电子迭代快速收敛;
2) 对于某些磁性金属体系,使用过大的 AMIX 值(比如 AMIX = 0.3)时,虽然也会使得电子迭代快速收敛,但此时体系其实是收敛到更高的磁态上,当使用 AMIX = 0.02 进行迭代时,将获得能量更低的状态。具体例子见下面磁性金属 MIXING 测试结果;
3) 对于磁性材料,特别是结构较复杂、电子迭代不容易收敛的体系,建议扫描 AMIX 值。
4、在 PBE 计算时,OUTCAR 文件中会给出 “average eigenvalue” 的信息,见下面图片。对于“线性混合”,手册认为当该值为 1 时,对应的电荷密度混合最好,电子迭代最好。据此手册给出了一个获得最佳 AMIX 的方法:使用要给 AMIX 值进行迭代计算,然后搜索 OUTCAR 中“average eigenvalue”的数值 Γ,优化的 AMIX 为:AMIXopt = AMIXcurrent * Γ,然后用新的 AMIXopt 值做电子迭代,直至 Γ = 1。

5、相比于手册推荐的方法,我个人更推荐直接扫描 AMIX 值(比如从 0.02 扫到 0.2,间隔取 0.02)。对此磁性金属体系,使用手册的方法优化 AMIX,有时会给出相当糟糕的结果。见下文的测试例子。
磁性金属 MIXING 测试结果
1、第一个测试例子:这里给出两个磁性金属体系 b1 和 b1_9 的测试结果,其中 b1_9 中含有多层过渡金属层,通过 MAGMOM 设置了层间反铁磁耦合。测试内容为:测试 NBANDS、k-spacing 和 AMIX 对体系电子迭代的影响。其他参数:PREC = Normal,ENCUT = 400,ALGO = Normal,ISMEAR = 1,SIGMA = 0.1,NELM = 80。
1) 以下结果的说明:
a) 设置电子迭代步数最大为 81(NELM = 81);
b) AMIX:所用的 AMIX 值;
c) NUM:电子迭代步数;
d) Γ1:计算完成后从 OUTCAR 中提取 Γ 值,使用最后三个 Γ 值的平均值代入 AMIXopt = AMIXcurrent * Γ 中产生下一步的 AMIX 值,在此仅展示三个 Γ 值中的一个;
e) MAG:OSZICAR 给出的体系总磁矩;
f) E0: 体系能量;
g) 标淡黄色的部分表示计算正确收敛到了磁态上。
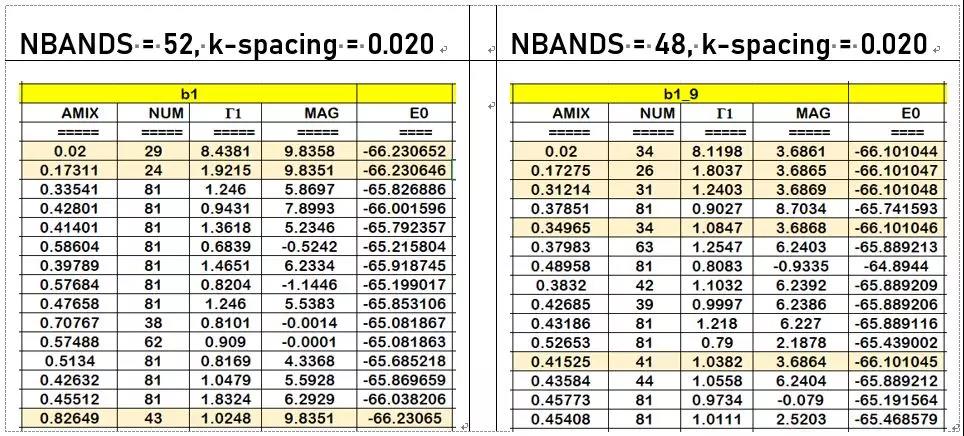
2) 对照组,按照手册的方法以 Γ = 1 为目标优化 AMIX 值:
NBANDS = 52, k-spacing = 0.020 NBANDS = 48, k-spacing = 0.020
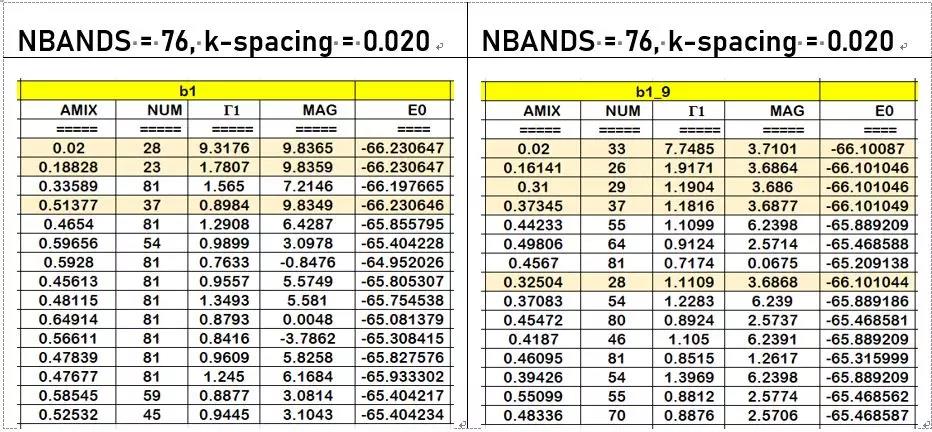
3) 增大 NBANDS,按照手册的方法以 Γ = 1 为目标优化 AMIX 值:
NBANDS = 76, k-spacing = 0.020 NBANDS = 76, k-spacing = 0.020
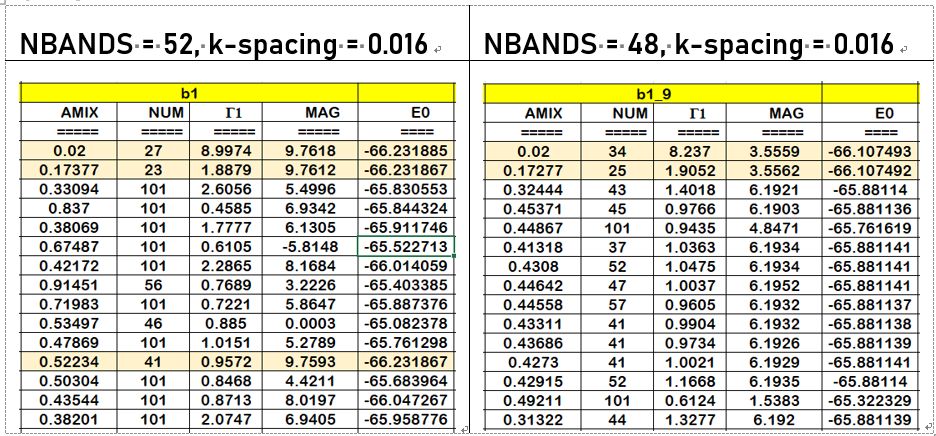
4) 减小 k-spcing,按照手册的方法以 Γ = 1 为目标优化 AMIX 值:
NBANDS = 52, k-spacing = 0.016 NBANDS = 48, k-spacing = 0.016
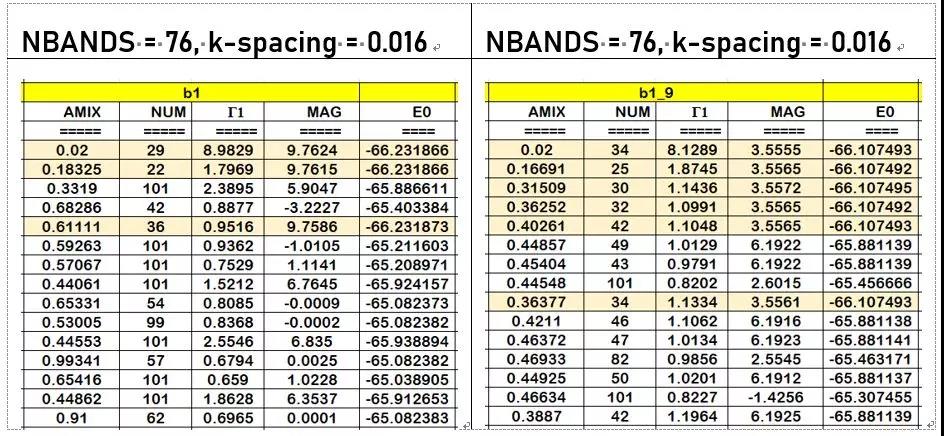
5) 增大 NBANDS + 减小 k-spacing,按照手册的方法以 Γ = 1 为目标优化 AMIX 值:
NBANDS = 76, k-spacing = 0.016 NBANDS = 76, k-spacing = 0.016
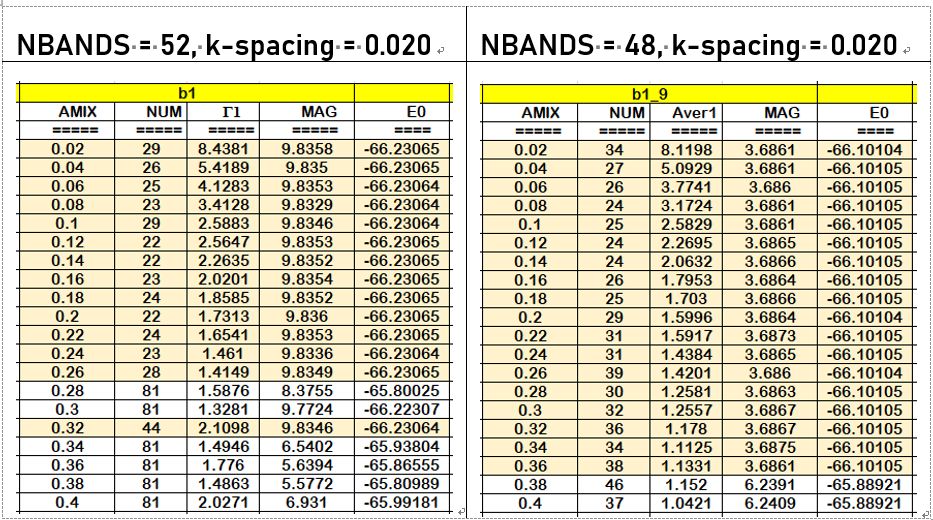
6) 扫描 AMIX 值:
NBANDS = 52, k-spacing = 0.020 NBANDS = 48, k-spacing = 0.020
7) 从以上结果可以看到:
a) 在 b1 和 b1_9 这两个体系中,使用手册所给的方法很难得到合适的 AMIX 值;
b) 对于这两个磁性金属体系,当 AMIX 值设置不合理(过大)时,体系将不收敛,或者收敛到更高的状态上(与能量更低的状态相比,体系能量和总磁矩均有很大差异)。需要取较小的 AMIX 值,才能收敛到更低的磁态;
c) 特别是对于 b1_9 体系,在设置了层间反铁磁耦合或,当 AMIX 值设置不合理时,将无法获得需要的层间反铁磁耦合态;
d) 需要注意的是,若不设置 MIXING,VASP 默认使用 AMIX = 0.4 (默认 BMIX = 1.0),这一数值对于 b1 和 b1_9 来说可能是过大的;
e) NBANDS 和 k-spacing 足够大以后,再增大 NBANDS 和 k-spacing 对体系收敛性提升不大。对于较大的 AMIX 值,自洽计算依然不收敛或者收敛错误。
2、第二个测试例子:ca1_5 通过 MAGMOM 设置为反铁磁耦合,为磁性金属。在进行结构优化时,k-spacing = 0.02,PREC = Normal,ISMEAR = 0,SIGMA = 0.1,ENCUT = 500。对比 AMIX 值对电子迭代的影响。
| MIXING 参数 | 结果 |
|---|---|
| AMIX = 0.2;BMIX= 0.0001;BMIX_MAG = 0.0001 | 第一步离子步跑了200步不收敛;磁态变成亚铁磁 |
| AMIX = 0.02;BMIX = 0.0001;BMIX_MAG = 0.0001 | 第一步离子步跑了120步收敛;磁态保持反铁磁 |
在这一体系中,对于 AMIX 更加敏感,相对于上面的 b1 和 b1_9 体系,使用 AMIX = 0.2 自洽计算无法收敛,需要使用更小的 AMIX 值。
总结
1) 相比于非磁体系,磁性体系的自洽迭代常常会遇到难以收敛的问题。使用“线性混合”的方法能有效改善磁性体系的收敛情况;
2) 判断体系为金属还是半导体后,选择 ALGO (一般使用 ALGO = Normal 即可)和 AMIX 值。对于磁性金属体系和磁性半导体,个人(在 ALGO = Normal 基础上)常设置的 AMIX 值分别为 0.02 和 0.2;
3) 若要进一步优化 AMIX 值,建议进行 AMIX 扫描。
转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。